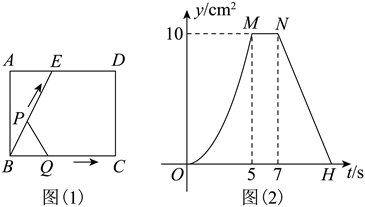
如图 (1) 所示, $E$ 为矩形 $A B C D$ 的边 $A D$ 上一点, 动点 $P, Q$ 同时从点 $B$ 出发, 点 $P$ 沿折线 $B E-E D-D C$ 运动到点 $C$ 时停止, 点 $Q$ 沿 $B C$ 运动到点 $C$ 时停止, 它们运动的速度都是 $1 cm /$秒, 设 $P 、 Q$ 同时出发 $t$ 秒时, $\triangle B P Q$ 的面积为 $y cm^2$. 已知 $y$ 与 $t$ 的函数关系图象如图 (2) (曲线 $O M$ 为抛物线的一部分) 则下列结论错误的是

A. $A B=4 cm$
B. 当 $5 < t < 7$ 时, $\triangle B P Q$ 的面积是定值
C. 当 $0 < t \leq 5$ 时, $y=\frac{4}{5} t^2$
D. 当 $t=\frac{29}{4}$ 秒时, $\frac{B Q}{P Q}=\frac{4}{3}$