2022年河南省中考数学真题

导出试卷

打印试卷试卷白板

2022年河南省中考数学真题

单选题（共 10 题），每题只有一个选项正确

$-\frac{1}{2}$ 的相反数是 ( )

$\text{A.}$ $\frac{1}{2}$ $\text{B.}$ $2$ $\text{C.}$ $-2$ $\text{D.}$ $-\frac{1}{2}$

查看分享编辑下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

2022年北京冬奥会的奖牌 “同心” 表达了 “天地合 -人心同” 的中华文化内涵.将这六个汉字分别写在某正方体的表面上, 如图是它的一种展开图, 则在原正方体中, 与 “地” 字所在面相对的面上的汉字是

$\text{A.}$ 合 $\text{B.}$ 同 $\text{C.}$ 心 $\text{D.}$ 人

查看分享编辑下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

如图, 直线 $\mathrm{AB}, \mathrm{CD}$ 相交于点 $\mathrm{O}, \mathrm{E} O \perp \mathrm{CD}$, 垂足为 $\mathrm{O}$. 若 $\angle \mathbf{1}=\mathbf{5 4}^{\circ}$, 则 $\angle 2$ 的度数为

$\text{A.}$ $26^{\circ}$ $\text{B.}$ $36^{\circ}$ $\text{C.}$ $44^{\circ}$ $\text{D.}$ $54^{\circ}$

查看分享编辑下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

下列运算正确的是（）

$\text{A.}$ $2 \sqrt{3}-\sqrt{3}=\mathbf{2}$ $\text{B.}$ $(a+1)^2=a^2+1$ $\text{C.}$ $\left(a^2\right)^3=a^5$ $\text{D.}$ $2 a^2 \cdot a=2 a^3$

查看分享编辑下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

如图, 在菱形 $A B C D$ 中, 对角线 $A C, B D$ 相交于点 $O$, 点 $E$ 为 $C D$ 的中点. 若 $O E=3$, 则菱形 $A B C D$ 的周长为

$\text{A.}$ 6 $\text{B.}$ 12 $\text{C.}$ 24 $\text{D.}$ 48

查看分享编辑下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

一元二次方程 $x^2+x-1=0$ 的根的情况是

$\text{A.}$ 有两个不相等的实数根 $\text{B.}$ 没有实数根 $\text{C.}$ 有两个相等的实数根 $\text{D.}$ 只有一个实数根

查看分享编辑下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

如图所示的扇形统计图描述了某校学生对课后延时服务的打分情况 (满分 5 分), 则所打分数的众数为

$\text{A.}$ 5 分 $\text{B.}$ 4 分 $\text{C.}$ 3 分 $\text{D.}$ $45 \%$

查看分享编辑下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

《孙子算经》中记载: “凡大数之法, 万万日亿, 万万亿日兆.” 说明了大数之间的关系: 1 亿 $=1$ 万 $\times 1$ 万, 1 兆 $=1$ 万 $\times 1$ 万 $\times 1$ 亿. 则 1 兆等于（）

$\text{A.}$ $10^8$ $\text{B.}$ $10^{12}$ $\text{C.}$ $10^{16}$ $\text{D.}$ $10^{24}$

查看分享编辑下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

如图, 在平面直角坐标系中, 边长为 2 的正六边形 ABCDEF 的中心与原点 $O$ 重合, $\mathbf{A B} / / \mathbf{x}$ 轴, 交 $\mathbf{y}$ 轴于点 $\mathbf{P}$, 将 $\triangle O A P$ 绕点 $O$ 顺时针旋转, 每次旋转 $90^{\circ}$, 则第 2022 次旋转结束时, 点 $\mathrm{A}$ 的坐标为

$\text{A.}$ $(\sqrt{3},-1)$ $\text{B.}$ $(-{1},-\sqrt{3})$ $\text{C.}$ $(-\sqrt{3},-1)$ $\text{D.}$ $({1}, \sqrt{3})$

查看分享编辑下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

呼气式酒精测试仪中装有酒精气体传感器, 可用于检测驾驶员是否酒后驾车, 酒精气体传感器是一种气敏电阻（图 1 中的 $R_1$ ), $R_1$ 的阻值随呼气酒精浓度 $K$ 的变化而变化 (如图 2), 血液酒精浓度 $M$ 与呼气酒精浓度 $K$ 的关系见图 3.下列说法不正确的是

$\text{A.}$ 呼气酒精浓度 $K$ 越大, $R_1$ 的阻值越小 $\text{B.}$ 当 $K=0$ 时, $R_1$ 的阻值为 100 $\text{C.}$ 当 $K=10$ 时, 该驾驶员为非酒驾状态 $\text{D.}$ 当 $R_1=20$ 时, 该驾驶员为醉驾状态

查看分享编辑下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

填空题（共 5 题），请把答案直接填写在答题纸上

请写出一个 $y$ 随 $x$ 的增大而增大的一次函数的表达式:

查看分享编辑下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

不等式组 $\left\{\begin{array}{l}x-3 \leqslant 0, \\ \frac{x}{2}>1\end{array}\right.$ 的解集为

查看分享编辑下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

为开展 “喜迎二十大、永远跟党走、奋进新征程” 主题教育宣讲活动, 某单位从甲、乙、丙、丁四名宣讲员中随机选取两名进行宣讲, 则恰好选中甲和丙的概率为

查看分享编辑下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

如图, 将扇形 $\mathrm{AOB}$ 沿 $\mathrm{OB}$ 方向平移, 使点 $\mathrm{O}$ 移到 $\mathrm{OB}$ 的中点 $\mathrm{O}^{\prime}$ 处, 得到扇形 $\mathbf{A}^{\prime} \mathrm{O}^{\prime} \mathrm{B}^{\prime}$. 若 $\angle \mathrm{O}=90^{\circ}, \mathrm{OA}=\mathbf{2}$, 则阴影部分的面积为

查看分享编辑下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

如图, 在 Rt $\triangle \mathbf{A B C}$ 中, $\angle \mathbf{A C B}=90^{\circ}, \mathbf{A C}=\mathbf{B C}=2 \sqrt{2}$, 点 $\mathbf{D}$ 为 $\mathbf{A B}$ 的中点, 点 $P$ 在 $\mathbf{A C}$ 上, 且 $\mathbf{C P}=1$, 将 $\mathrm{CP}$ 绕点 $\mathrm{C}$ 在平面内旋转, 点 $P$ 的对应点为点 $Q$, 连接 $A Q, D Q$. 当 $\angle A D Q=90^{\circ}$ 时, $A Q$ 的长为

查看分享编辑下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

解答题（共 8 题），解答过程应写出必要的文字说明、证明过程或演算步骤

（1）计算: $\sqrt[3]{27}-\left(\frac{1}{3}\right)^0+2^{-1}$;
（2）化简: $\frac{x^2-1}{x} \div\left(1-\frac{1}{x}\right)$.

查看分享编辑下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

2022 年 3 月 23 日下午, “天言课堂”第二课在中国空间站开讲, 神舟十三号乘组航天员翟志刚、王亚平、叶光富相互配合进行授课, 这是中国空间站的第二次太空授课, 被许多中小学生称为“最牛网课”. 某中学为了解学生对 “航空航天知识” 的掌握情况, 随机抽取 50 名学生进行测试, 并对成绩 (百分制) 进行整理, 信息如下:
a. 成绩频数分布表:

b. 成绩在 $70 \leqslant \mathbf{x} < 80$ 这一组的是（单位: 分):
$\begin{array}{llllllllllll}70 & 71 & 72 & 72 & 74 & 77 & 78 & 78 & 78 & 79 & 79 & 79\end{array}$ 根据以上信息, 回答下列问题:
（1）在这次测试中, 成绩的中位数是分, 成绩不低于 $\mathbf{8 0}$ 分的人数占测试人数的百分比为
（2）这次测试成绩的平均数是 $76.4$ 分, 甲的测试成绩是 77 分.乙说: “甲的成绩高于平均数, 所以甲的成绩高于一半学生的成绩.” 你认为乙的说法正确吗? 请说明理由・
（3）请对该校学生 “航空航天知识” 的掌握情况作出合理的评价.

查看分享编辑下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

如图, 反比例函数 $y=\frac{\mathrm{k}}{\mathrm{x}}(x>0)$ 的图象经过点 $\mathrm{A}(2,4)$ 和点 $\mathrm{B}$, 点 $\mathrm{B}$ 在点 $\mathrm{A}$ 的下方, $\mathrm{AC}$ 平分 $\angle O A B$, 交 $\mathrm{x}$ 轴于点 $\mathrm{C}$.
（1）求反比例函数的表达式
（2）请用无刻度的直尺和圆规作出线段 $\mathrm{AC}$ 的垂直平分线. (要求: 不写作法, 保留作图痕迹)
(3) 线段 $\mathrm{OA}$ 与 (2) 中所作的垂直平分线相交于点 D. 连接 $\mathrm{CD}$. 求证： $\mathbf{C D} / / \mathbf{A B}$.

查看分享编辑下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

开封清明上河图是依照北宋著名画家张择端的《清明上河图》建造的, 拂云阁是园内最高的建筑, 某数学小组测量拂云阁 DC 的高度如图, 在 $A$ 处用测角仪测得拂云阁顶端 $\mathrm{D}$ 的仰角为 $34^{\circ}$, 沿 $\mathrm{AC}$ 方向前进 $15 \mathrm{~m}$ 到达 $B$ 处, 又测得拂云阁顶端 $\mathrm{D}$ 的仰角为 $45^{\circ}$. 已知测角仪的高度为 $1.5 \mathrm{~m}$, 测量点 $A, B$ 与拂云阁 $D C$ 的底部 $C$ 在同一水平线上, 求拂云阁 DC 的高度（结果精确到 $1 \mathrm{~m}$. 参考数据: $\sin 34^{\circ}$ $\left.\approx 0.56, \cos 34^{\circ} \approx 0.83, \tan 34^{\circ} \approx 0.67\right)$

查看分享编辑下载此题点赞(0) 收藏(1) 错题本(1) 白板加入试卷

近日, 教育部印发《义务教育课程方案》和课程标准 (2022 年版), 将劳动从原来的综合实践活动课程中独立出来. 某中学为了让学生体验农耕劳动, 开辟了一处耕种园, 需要采购一批菜苗开展种植活动,据了解，市场上每捆 $A$ 种菜苗的价格是菜亩基地的 $\frac{5}{4}$ 倍, 用 300 元在市场上购头的 $A$种菜苗比在菜苗基地购买的少3捆
（1）求菜苗基地每捆 $A$ 种菜苗的价格.
（2）菜苗基地每捆 $B$ 种菜苗的价格是 30 元. 学校决定在菜苗基地购头 $A, B$ 两种菜苗共 100 捆, 且 $A$ 种菜苗的捆数不超过 $B$ 种菜苗的捆数. 菜苗基地为支持该校活动, 对 $A, B$ 两种菜苗均提供九折优惠. 求本次购买最少花费多少钱.

查看分享编辑下载此题点赞(1) 收藏(0) 错题本(0) 白板加入试卷

小红看到一处喷水景观, 喷出的水柱呈抛物线形状, 她对此展开研究: 测得喷水头 $P$ 距地面 $0.7 \mathrm{~m}$, 水柱在距喷水头 $P$ 水平距离 $5 \mathrm{~m}$ 处达到最高, 最高点距地面 $3.2 \mathrm{~m}$; 建立如图所示的平面直角坐标系, 并设抛物线的表达式为 $y=a(x-h)^2+k$, 其中 $x(m)$ 是水柱距喷水头的水平距离, $y(m)$ 是水柱距地面的高度.
（1）求抛物线的表达式.
（2）爸爸站在水柱正下方, 且距喷水头 $P$ 水平距离 $3 \mathrm{~m}$. 身高 $1.6 \mathrm{~m}$ 的小红在水柱下方䞢动, 当她的头页恰好接触到水柱时, 求她与爸爸的水平距离.

查看分享编辑下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

为弘扬民族传统体育文化, 某校将传统游戏 “滚铁环” 列入了校运动会的比赛项日. 滚铁环器材山铁环和推杆组成. 小明对滚铁环的启动阶段进行了研究, 如图, 滚铁环时, 铁环 $\odot O$ 与水平地面相切于点 $C$, 推杆 $A B$ 与铅垂线 $A D$ 的夹角为 $\angle B A D$, 点 $O, A, B, C, D$ 在同一平面内. 当推杆 $A B$ 与铁环 $\odot O$ 相切于点 $B$ 时, 手上的力量通过切点 $B$ 传递到铁环上,会有较好的启动效果.

(1) 求证: $\angle \mathrm{BOC}+\angle \mathrm{BAD}=\mathbf{9 0}^{\circ}$.
(2) 实践中发现, 切点 $\mathbf{B}$ 只有在铁环上一定区域内时, 才能保证铁环平稳启动. 图中点 $\mathrm{B}$ 是该区域内最低位置, 此时点 $\mathbf{A}$ 距地面的距离 $\mathrm{AD}$ 最测得 $\cos \angle B A D=\frac{3}{5}$. 已知铁环 $\odot O$ 的半径为 $25 \mathrm{~cm}$, 推杆 $A B$ 的长为 $75 \mathrm{~cm}$, 求此时 $A D$ 的长.

查看分享编辑下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

综合与实践
综合与实践课上, 老师让同学们以 “矩形的折叠” 为主题开展数学活动.
(1) 操作判断
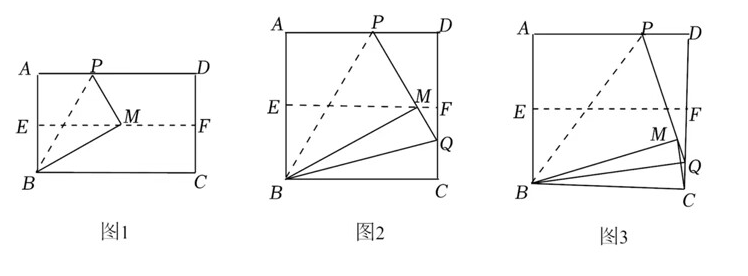
操作一: 对折矩形纸片 $\mathbf{A B C D}$, 使 $\mathbf{A D}$ 与 $\mathbf{B C}$ 重合, 得到折痕 $\mathbf{E F}$, 把纸片展平;
操作二: 在 $A D$ 上选一点 $P$, 沿 $B P$ 折叠, 使点 $A$ 落在矩形内部点 $M$ 处, 把纸片展平, 连接 PM, BM.
根据以上操作, 当点 $M$ 在 $E F$ 上时, 写出图 1 中一个 $30^{\circ}$ 的角:
(2) 迁移探究
小华将矩形纸片换成正方形纸片, 继续探究, 过程如下: 将正方形纸片 $\mathbf{A B C D}$ 按照 (I) 中的方式操作, 并延长 $\mathbf{P M}$ 交 $\mathrm{CD}$ 于点 $Q$, 连接 $B Q$.
(1)如图 2, 当点 $\mathrm{M}$ 在 $\mathbf{E F}$ 上时, $\angle \mathrm{MBQ}=\quad, \angle \mathrm{CBQ}=$
(2)改变点 $P$ 在 $\mathbf{A D}$ 上的位置 (点 $\mathbf{P}$ 不与点 $\mathbf{A}, \mathbf{D}$ 重合), 如图 3, 判断 $\angle \mathrm{MBQ}$ 与 $\angle \mathrm{CBQ}$ 的数量关系, 并说明理由.
(3) 拓展应用
在 (2) 的探究中, 已知正方形纸片 $A B C D$ 的边长为 $8 \mathrm{~cm}$, 当 $F Q=1 \mathrm{~cm}$ 时, 直接写出 $\mathbf{A P}$ 的长.

查看分享编辑下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

非会员每天可以查看15道试题。开通会员，海量试题无限制查看。

无限看试题
下载试题
组卷

开通会员

热点推荐

试卷二维码

分享此二维码到群，让更多朋友参与

试卷白板

试卷白板提供了一个简单的触摸书写板，可供老师上课、或者视频直播时，直接利用白板给学生讲解试题，如有意见，欢迎反馈。