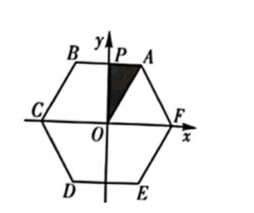
如图, 在平面直角坐标系中, 边长为 2 的正六边形 ABCDEF 的中 心与原点 $O$ 重合, $\mathbf{A B} / / \mathbf{x}$ 轴, 交 $\mathbf{y}$ 轴于点 $\mathbf{P}$, 将 $\triangle O A P$ 绕点 $O$ 顺时针旋转, 每次旋转 $90^{\circ}$, 则第 2022 次旋转结束时, 点 $\mathrm{A}$ 的 坐标为

A. $(\sqrt{3},-1)$
B. $(-{1},-\sqrt{3})$
C. $(-\sqrt{3},-1)$
D. $({1}, \sqrt{3})$