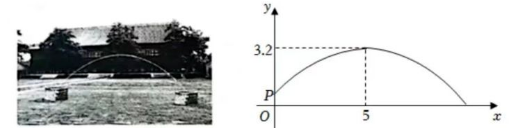
小红看到一处喷水景观, 喷出的水柱呈抛物线形状, 她对此展开研究: 测得喷水头 $P$ 距地面 $0.7 \mathrm{~m}$, 水柱在距喷水头 $P$ 水平距离 $5 \mathrm{~m}$ 处达到最高, 最高点距地面 $3.2 \mathrm{~m}$; 建立如图所示的平面直角坐 标系, 并设抛物线的表达式为 $y=a(x-h)^2+k$, 其中 $x(m)$ 是水柱距喷水头的水平距离, $y(m)$ 是 水柱距地面的高度.
（1）求抛物线的表达式.
（2）爸爸站在水柱正下方, 且距喷水头 $P$ 水平距离 $3 \mathrm{~m}$. 身高 $1.6 \mathrm{~m}$ 的小红在水柱下方䞢动, 当她的 头页恰好接触到水柱时, 求她与爸爸的水平距离.