单选题 (共 12 题 ),每题只有一个选项正确
已知集合 $A=\{-2,-1,0,1,2\}, B=\left\{x \mid x^2+x-2 < 0\right\}$, 则 $A \cap B=$
$\text{A.}$ $\{-1,0,1\}$
$\text{B.}$ $\{-1,0\}$
$\text{C.}$ $\{-2,-1,1,2\}$
$\text{D.}$ $\{0,1,2\}$
复数 $\frac{1}{1+2 \mathrm{i}}$ 的虚部是
$\text{A.}$ $-\frac{2}{5}$
$\text{B.}$ $-\frac{1}{5}$
$\text{C.}$ $\frac{1}{5}$
$\text{D.}$ $\frac{2}{5}$
抛物线 $y^2=2 x$ 的焦点到准线的距离为
$\text{A.}$ 4
$\text{B.}$ 2
$\text{C.}$ 1
$\text{D.}$ $\frac{1}{2}$
若变量 $ x, y $满足约束条件 $
\left\{\begin{array}{l}
x+y \leq 2 \\
y-x \leq 0, \\
y \geq 0
\end{array}\right. $ , 则 $z=x+2y$ 的最大值为
$\text{A.}$ 0
$\text{B.}$ 1
$\text{C.}$ 2
$\text{D.}$ 3
“$a b>0$” 是 “ $\frac{b}{a}+\frac{a}{b} \geq 2$” 的
$\text{A.}$ 充分不必要条件
$\text{B.}$ 必要不充分条件
$\text{C.}$ 充要条件
$\text{D.}$ 既不充分也不必要条件
已知点 $A, B, C$ 是球 $O$ 的小圆 $O^{\prime}$ 上的三点, 若 $A B=B C=C A=3 \sqrt{3}, O O^{\prime}=4$, 则球 $O$ 的 表面积为
$\text{A.}$ $64 \pi$
$\text{B.}$ $100 \pi$
$\text{C.}$ $144 \pi$
$\text{D.}$ $200 \pi$
若直线 $x=2 \sqrt{2} y-3 \sqrt{2}$ 与圆 $x^2+y^2=4$ 相交于 $A, B$ 两点, $O$ 为坐标原点, 则 $\overrightarrow{O A} \cdot \overrightarrow{A B}=$
$\text{A.}$ $2 \sqrt{2}$
$\text{B.}$ $ 4$
$\text{C.}$ $-2 \sqrt{2}$
$\text{D.}$ $-4$
如图, 正四棱台 $A B C D-A_1 B_1 C_1 D_1$ 中, 点 $E, F, G$ 分别是 棱 $C_1 D_1, D_1 A_1, A_1 B_1$ 的中点, 则下列判断中, 不正确的是
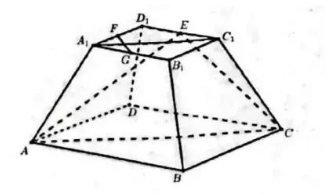
$\text{A.}$ $B, B_1, D_1, D$ 共面
$\text{B.}$ $F \in$ 平面 $A C E$
$\text{C.}$ $F G \perp$ 平面 $A C E$
$\text{D.}$ $A_1 C_1 / /$ 平面 $A C E$
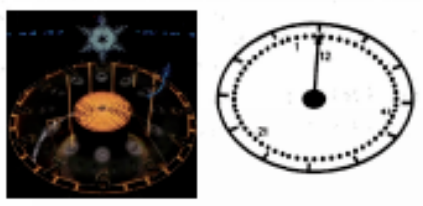
9. 冬残奥会闭幕式上, 中国式浪漫再现, 天干地支时辰钟表盘再现, 由定音鼓构成的“表盘” 形象上, 60 名残健共融表演者用行为模拟“指针”每圈 60 个时间刻度的行进轨 迹.若以图中 12 点与圆心连线为始边, 某时刻指向第 $1,21,41$ 名残健共融表演 者的“指针”为终边的角分别记为 $\alpha, \beta, \gamma$, 则 $\cos \alpha+\cos \beta+\cos \gamma$ 的值为
$\text{A.}$ $-1$
$\text{B.}$ $0$
$\text{C.}$ $1$
$\text{D.}$ $\cos \alpha$
设函数 $f(x)$ 的定义域为 $R$, 且 $f(x+2)$ 是奇函数, $f(x+1)$ 是偶函数, 则一定有
$\text{A.}$ $f(4)=0$
$\text{B.}$ $f(-1)=0$
$\text{C.}$ $f(3)=0$
$\text{D.}$ $f(5)=0$
若 $2 x-1=\sqrt{(x-2)^2+y^2}$, 则 $\sqrt{(x+2)^2+y^2}+\sqrt{(x-2)^2+y^2}$ 的最小值是
$\text{A.}$ 1
$\text{B.}$ 2
$\text{C.}$ 3
$\text{D.}$ 4
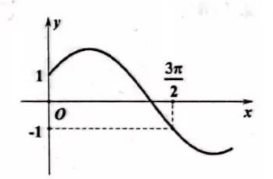
已知函数 $f(x)=2 \sin (\omega x+\varphi)$ 的部分图象如图, 则下列判断正确的是
$\text{A.}$ 函数 $f(x)$ 的周期为 $4 \pi$
$\text{B.}$ 对任意的 $x \in \mathrm{R}$, 都有 $f(x) \leq f\left(\frac{2 \pi}{3}\right)$
$\text{C.}$ 函数 $f(x)$ 在区间 $[0,5 \pi]$ 上恰好有三个零点
$\text{D.}$ 函数 $f\left(x-\frac{\pi}{4}\right)$ 是偶函数
填空题 (共 4 题 ),请把答案直接填写在答题纸上
若函数 $f(x)=(x+a) \sin x$ 在 $x=\pi$ 时取得极值, 则 $a=$
执行如下程序框图, 输出 $i$ 的值为
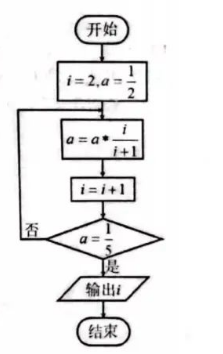
某工厂 10 名工人某天生产同一类型零件, 生产的件数分别 是 $7,8,9,10,11,12,12,12,13,14$, 则这组数据的方差为 (参考数据: 这组数据的平方和为 1212 )
已知 $\overrightarrow{O A}, \overrightarrow{O C}$ 为正交基底, 且 $\overrightarrow{O B}=\lambda \overrightarrow{O A}, \overrightarrow{O D}=\mu \overrightarrow{O C}, \lambda>\mu>1$, $P, Q$ 分别为 $A C, B D$ 的中点, 若 $|\overrightarrow{A B} \| \overrightarrow{C D}|=1$, 则 $|\overrightarrow{P Q}|$ 的最小值为
解答题 (共 7 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
已知公差大于 0 的等差数列 $\left\{a_n\right\}$ 满足 $a_1=1$, 且 $a_1, a_2, a_4$ 成等比数列.
(1) 求数列 $\left\{a_n\right\}$ 的通项公式:
(2) 令 $b_n=2^{a_{2 n}}$, 求数列 $\left\{b_n\right\}$ 的前 $n$ 项和.
如图是飞行棋部分棋盘图示, 飞机的初始位置为 0 号格, 抛郑一个质地均匀的骰子,若抛出的点数为 1,2 , 飞机在原地不动:若拋出的点数为 3,4 , 飞机向前移一格; 若抛 出的点数为 5,6 ,飞机向前移两格. 记扡掷一次骰子后,飞机到达 1 号格为事件 $A$, 记抛两次 骰子后, 飞机到达 2 号格为事件 $B$.
(1) 求 $P(A)$;
(2) 求 $P(B)$.

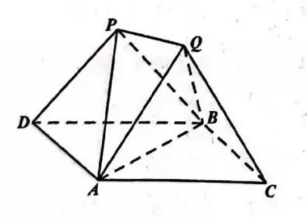
如图, 桌面上拱放了两个相同的正四面体 $P A B D$ 和 $Q A B C$
(1) 求证: $P Q \perp A B$;
(2) 若 $A B=2$, 求四面体 $A P Q B$ 的体积.
已知函数 $f(x)=\mathrm{e}^x+(1-a) x-\ln a \cdot \ln x(a>0)$.
(1)若 $a=\mathrm{e}$, 求函数 $f(x)$ 的极值;
(2) 讨论函数 $f(x)$ 的单调性.
已知 $A(2,0), B(0,1)$ 是椭圆 $E: \frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$ 的两个顶点.
(1) 求椭圆 $E$ 的标准方程;
(2) 过点 $P(2,1)$ 的直线 $l$ 与椭圆 $E$ 交于 $C, D$, 与直线 $A B$ 交于点 $M$, 求 $\frac{|P M|}{|P C|}+\frac{|P M|}{|P D|}$ 的 值.
已知曲线 $C_1$ 的参数方程为 $\left\{\begin{array}{l}x=t \\ y=\sqrt{3} t\end{array}\right.$ ( $t$ 为参数), 以 $O$ 为极点, $x$ 轴的非负半轴为极轴, 建立 极坐标系, 曲线 $C_2$ 的极坐标方程为 $\rho=\frac{2}{1-\sin \theta}$.
(1) 求曲线 $C_1$ 的普通方程, 曲线 $C_2$ 的直角坐标方程;
(2) 设曲线 $C_1, C_2$ 的交点为 $A, B$, 求 $|A B|$ 的值.
已知函数 $f(x)=|2 x-6|-|3 x-6|$.
(1)求不等式 $f(x)>1$ 的解集;
(2) 若不等式 $f(x) \leq k|x|$ 恒成立, 求实数 $k$ 的取值范围.