单选题 (共 16 题 ),每题只有一个选项正确
函数 $\mathrm{f}({x})=\sin {x}+\cos {x}$ 的最小正周期是
$\text{A.}$ $2 \pi$
$\text{B.}$ $2 \sqrt{2} \pi$
$\text{C.}$ $\pi$
$\text{D.}$ $\frac{\pi}{4}$
如果双曲线的焦距为 6 , 两条准线间的距离为 4 , 那么该双曲线的离心率为
$\text{A.}$ $\frac{3}{2}$
$\text{B.}$ $\frac{\sqrt{3}}{2}$
$\text{C.}$ $\frac{\sqrt{6}}{2}$
$\text{D.}$ 2
和直线 $3 x-4 y+5=0$ 关于 $x$ 轴对称的直线的方程为
$\text{A.}$ $3 x+4 y-5=0$
$\text{B.}$ $3 x+4 y+5=0$
$\text{C.}$ $-3 x+4 y-5=0$
$\text{D.}$ $-3 x+4 y+5=0$
$y=x^{\frac{3}{5}}$ 在 $[-1,1]$ 上是
$\text{A.}$ 增函数且是奇函数
$\text{B.}$ 增函数且是偶函数
$\text{C.}$ 减函数且是奇函数
$\text{D.}$ 减函数且是偶函数
$\lim _{n \rightarrow \infty} \frac{5 n^2-1}{2 n^2-n+5}$ 的值为
$\text{A.}$ $-\frac{1}{5}$
$\text{B.}$ $-\frac{5}{2}$
$\text{C.}$ $\frac{1}{5}$
$\text{D.}$ $\frac{5}{2}$
设集合 $M=\left\{x \left\lvert\, x=\frac{k}{2}+\frac{1}{4}\right., k \in Z\right\}, N=\left\{x \left\lvert\, x=\frac{k}{4}+\frac{1}{2}\right., k \in Z\right\}$, 则
$\text{A.}$ $\mathrm{M}=\mathrm{N}$
$\text{B.}$ $\mathrm{M} \subset \mathrm{N}$
$\text{C.}$ $\mathrm{M} \supset \mathrm{N}$
$\text{D.}$ $\mathrm{M} \cap \mathrm{N}=\Phi$
$\sin 20^{\circ} \cos 70^{\circ}+\sin 10^{\circ} \sin 50^{\circ}$ 的值是
$\text{A.}$ $\frac{1}{4}$
$\text{B.}$ $\frac{\sqrt{3}}{2}$
$\text{C.}$ $\frac{1}{2}$
$\text{D.}$ $\frac{\sqrt{3}}{4}$
参数方程 $\left\{\begin{array}{l}x=\left|\cos \frac{\theta}{2}+\sin \frac{\theta}{2}\right| \\ y=\frac{1}{2}(1+\sin \theta)\end{array} \quad(0 < \theta < 2 \pi)\right.$ 表示
$\text{A.}$ 双曲线的一支, 这支过点$(1, \frac{1}{2} )$
$\text{B.}$ 抛物线的一部分, 这部分过点$(1, \frac{1}{2} )$
$\text{C.}$ 双曲线的一支, 这支过点$(-1, \frac{1}{2} )$
$\text{D.}$ 抛物线的一部分, 这部分过点$(-1, \frac{1}{2} )$
若 $a 、 b$ 是任意实数, 且 $a>b$, 则
$\text{A.}$ $a^2>b^2$
$\text{B.}$ $\frac{{b}}{{a}} < 1$
$\text{C.}$ $\lg (a-b)>0$
$\text{D.}$ $\left(\frac{1}{2}\right)^a < \left(\frac{1}{2}\right)^b$
一动圆与两圆 $x^2+y^2=1$ 和 $x^2+y^2-8 x+12=0$ 都外切, 则动圆圆心轨迹为
$\text{A.}$ 圆
$\text{B.}$ 椭圆
$\text{C.}$ 双曲线的一支
$\text{D.}$ 拋物线
圆柱轴截面的周长 1 为定值, 那么圆柱体积的最大值是
$\text{A.}$ $\left(\frac{1}{6}\right)^3 \pi$
$\text{B.}$ $\frac{1}{9}\left(\frac{1}{2}\right)^3 \pi$
$\text{C.}$ $\left(\frac{1}{4}\right)^3 \pi$
$\text{D.}$ $2\left(\frac{1}{4}\right)^3 \pi$
$(\sqrt{\mathrm{x}}+1)^4(\mathrm{x}-1)^5$ 展开式中 $\mathrm{x}^4$ 的系数为
$\text{A.}$ -40
$\text{B.}$ 10
$\text{C.}$ 40
$\text{D.}$ 45
直角梯形的一个内角为 $45^{\circ}$, 下底长为上底长的 $\frac{3}{2}$, 这个梯形绕下底所在的直线旋转一周所成的旋转体的全面积为 $(5+\sqrt{2}) \pi$, 则旋转体的体积为
$\text{A.}$ $2 \pi$
$\text{B.}$ $\frac{4+\sqrt{2}}{3} \pi$
$\text{C.}$ $\frac{5+\sqrt{2}}{3} \pi$
$\text{D.}$ $\frac{7}{3} \pi$
已知 $\mathrm{a}_1, \mathrm{a}_2, \cdots, \mathrm{a}_8$ 为各项都大于零的等比数列, 公式 $q \neq 1$, 则
$\text{A.}$ $\mathrm{a}_1+\mathrm{a}_8>\mathrm{a}_4+\mathrm{a}_5$
$\text{B.}$ $\mathrm{a}_1+\mathrm{a}_8 < \mathrm{a}_4+\mathrm{a}_5$
$\text{C.}$ $a_1+a_8=a_4+a_5$
$\text{D.}$ $a_1+a_8$ 和 $a_4+a_5$ 的大小关系不能由已知条件确定
设有如下三个命题:
甲: 相交直线 $1 、 m$ 都在平面 $a$ 内, 并且都不在平面 $\beta$ 内;
乙: 直线 $1 、 m$ 中至少有一条与平面 $\beta$ 相交;
丙: 平面 $a$ 与平面 $\beta$ 相交.
当甲成立时
$\text{A.}$ 乙是丙的充分而不必要条件
$\text{B.}$ 乙是丙的必要而不充分条件
$\text{C.}$ 乙是丙的充分且必要条件
$\text{D.}$ 乙既不是丙的充分条件又不是丙的必要条件
将数字 $1,2,3,4$ 填入标号为 $1,2,3,4$ 的四个方格里, 每格填一个数字, 则每个方格的标号与所填的数字均不相同的填法有
$\text{A.}$ 6 种
$\text{B.}$ 9 种
$\text{C.}$ 11 种
$\text{D.}$ 23 种
填空题 (共 5 题 ),请把答案直接填写在答题纸上
$\sin \left(\arccos \frac{1}{2}+\arccos \frac{1}{3}\right)=$
若双曲线 $\frac{x^2}{9 k^2}-\frac{y^2}{4 k^2}=1$ 与圆 $x^2+y^2=1$ 没有公共点, 则实数 $k$ 的取值范围为
从 $1,2, \cdots, 10$ 这十个数中取出四个数, 使它们的和为奇数, 共有 种取法(用数字作答)
建造一个容积为 $8 \mathrm{~m}^3$, 深为 2 m 的长方体无盖水池, 如果池底和池壁的造价每平方米分别为 120 元和 80 元,则水池的最低造价为
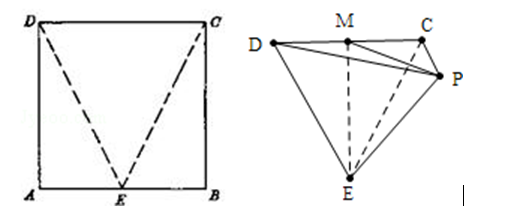
如图, $A B C D$ 是正方形, $E$ 是 $A B$ 的中点, 如将 $\triangle D A E$ 和 $\triangle C B E$ 分别沿虚线 $D E$ 和 $C E$ 折起, 使 $A E$ 与 $B E$ 重合, 记 $A$ 与 $B$ 重合后的点为 $P$, 则面 $P C D$ 与面 $E C D$ 所成的二面角为 ________ 度.
解答题 (共 6 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
已知 $f(x)=\log _a \frac{1+x}{1-x}(a>0, a \neq 1)$.
(1) 求 $\mathrm{f}(\mathrm{x})$ 的定义域;
(2) 判断 f (x)的奇偶性并予以证明;
(3) 求使 $f(x)>0$ 的 $x$ 取值范围.
已知数列 $\frac{8 \cdot 1}{1^2 \cdot 3^2}, \frac{8 \cdot 2}{3^2 \cdot 5^2}, \cdots, \frac{8 n}{(2 n-1)^2(2 n+1)^2}, \cdots . S_n$ 为其前 n 项和. 计算得 $S_1=\frac{8}{9}, \quad S_2=\frac{24}{25}, \quad S_3=\frac{48}{49}, \quad S_4=\frac{80}{81}$. 观察上述结果, 推测出计算 $S_n$ 的公式, 并用数学归纳法加以证明.
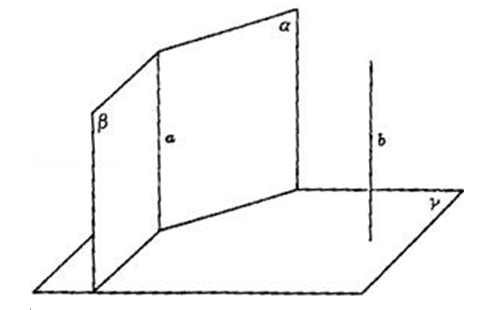
已知: 平面 $a \cap$ 平面 $\beta$ =直线 $a . a, \beta$ 同垂直于平面 $\gamma$, 又同平行于直线 $b$.
求证:
(1) $a \perp \gamma$;
(2) $\mathrm{b} \perp \gamma$.
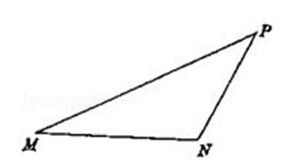
在面积为 1 的 $\triangle \mathrm{PMN}$ 中, $\tan \angle \mathrm{PMN}=\frac{1}{2}, \tan \angle \mathrm{MNP}=-2$. 建立适当的坐标系, 求以 $\mathrm{M}, \mathrm{N}$ 为焦点且过点 P 的椭圆方程.
设复数 $z=\cos \theta+i \sin \theta \quad(0 < \theta < \pi), \omega=\frac{1-(\bar{z})^4}{1+z^4}$, 并且 $|\omega|=\frac{\sqrt{3}}{3}, \arg \omega < \frac{\pi}{2}$, 求 $\theta$.
解方程 $\lg \left(x^2+4 x-26\right)-\lg (x-3)=1$.