单选题 (共 12 题 ),每题只有一个选项正确
设$2(z+\overline{z}) +3(z-\overline{z})=4+6i$,则$z=$ ( )
$\text{A.}$ $1-2i$
$\text{B.}$ $1+2i$
$\text{C.}$ $1+i$
$\text{D.}$ $1-i$
已知集合$S=\{s|s=2n+1,n \in Z\} $,$T=\{t|t=4n+1, n \in Z \}$ 则 $S \cap T= $ ( )
$\text{A.}$ $\phi$
$\text{B.}$ $S$
$\text{C.}$ $T$
$\text{D.}$ $Z$
3. 已知命题 $\mathrm{p}: \exists \mathrm{x} \in \mathrm{R}, \sin \mathrm{x} < 1$; 命题 $\mathrm{q}: \forall \mathrm{x} \in \mathrm{R}, e^{|x|} \geqslant 1$, 则下列命题中为真命 题的是()
$\text{A.}$ $\mathrm{p} \wedge \mathrm{q}$
$\text{B.}$ $\neg \mathrm{p} \wedge \mathrm{q}$
$\text{C.}$ $p \wedge \neg q$
$\text{D.}$ $\neg(\mathrm{pVq})$
设函数 $f(x)=\frac{1-x}{1+x}$, 则下列函数中为奇函数的是 ( )
$\text{A.}$ $f(x-1)-1$
$\text{B.}$ $\mathrm{f}(\mathrm{x}-1)+1$
$\text{C.}$ $\mathrm{f}(\mathrm{x}+1)-1$
$\text{D.}$ $f(x+1)+1$
在正方体 $A B C D-A_{i} B_{i} C_{:} D_{i}$ 中, $P$ 为 $B_{i} D_{i}$ 的中点, 则直线 $P B$ 与 $A D_{i}$ 所成的角为 ( )
$\text{A.}$ $\frac{\pi}{2}$
$\text{B.}$ $\frac{\pi}{3}$
$\text{C.}$ $\frac{\pi}{4}$
$\text{D.}$ $\frac{\pi}{6}$
将 5 名北京冬奥会志愿者分配到花样滑冰、短道速滑、冰球和冰显 4 个项目进 行培训, 每名志愿者只分到 1 个项目, 每个项目至少分配 1 名志愿者, 则不同的 分配方案共有 ( )
$\text{A.}$ 60 种
$\text{B.}$ 120 种
$\text{C.}$ 240 种
$\text{D.}$ 480 种
把函数 $y=f(x)$ 图象上所有点的横坐标缩短到原来的 $\frac{1}{2}$ 倍, 纵坐标不变, 再把所 得曲线向右平移 $\frac{\pi}{3}$ 个单位长度, 得到函数 $y=\sin \left(x-\frac{\pi}{4}\right)$ 的图像, 则 $f(x)=$ ( )
$\text{A.}$ $\sin \left(\frac{x}{2}-\frac{7 \pi}{12}\right)$
$\text{B.}$ $\sin \left(\frac{x}{2}+\frac{\pi}{12}\right)$
$\text{C.}$ $\sin \left(2 x-\frac{7 \pi}{12}\right)$
$\text{D.}$ $\sin \left(2 x+\frac{\pi}{12}\right)$
在区间 $(0,1)$ 与 $(1,2)$ 中各随机取 1 个数, 则两数之和大于 $\dfrac7 4$ 的概率为 ( )
$\text{A.}$ $\frac{7}{4}$
$\text{B.}$ $\frac{23}{32}$
$\text{C.}$ $\frac{9}{32}$
$\text{D.}$ $\frac{2}{9}$
魏晋时期刘徽撰写的《海岛算经》是关于测量的数学著作, 其中第一题是测量 海盗的高。如图, 点 $\mathrm{E}, \mathrm{H}, \mathrm{G}$ 在水平线 $\mathrm{AC}$ 上, $\mathrm{DE}$ 和 $\mathrm{FG}$ 是两个垂直于水平面且等 高的测量标杆的高度, 称为 “表高”, $\mathrm{EG}$ 称为 “表距”, $\mathrm{GC}$ 和 $\mathrm{EH}$ 都称为 “表目距”, $\mathrm{GC}$ 与 $\mathrm{EH}$ 的差称为 “表目距的差"。则海岛的高 $\mathrm{AB}=()$.
$\text{A.}$ $\dfrac{{表高} \times {表距}}{表目距的差} + 表高$
$\text{B.}$ $\dfrac{{表高} \times {表距}}{表目距的差} - 表高$
$\text{C.}$ $\dfrac{{表高} \times {表距}}{表目距的差} +表距$
$\text{D.}$ $\dfrac{{表高} \times {表距}}{表目距的差} -表距$
设 $a \neq 0$ ,若 $x=a$ 为函数 $f(x)=a(x-a)^{2}(x-h)$ 的㭁大值点 则 ( )
$\text{A.}$ $ a < b $
$\text{B.}$ $a > b $
$\text{C.}$ $a b < a^{2}$
$\text{D.}$ $a b > a^{2} $
设 $B$ 是椭圆 $C: \frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1(a>b>0)$ 的上顶点, 若 $C$ 上的任意一点 $P$ 都满 足 $|\mathrm{PB}| \leq 2 \mathrm{~b}$, 则 $\mathrm{C}$ 的离心率的取值范围是 ( )
$\text{A.}$ $\left[\frac{\sqrt{2}}{2}, 1\right)$
$\text{B.}$ $\left[\frac{1}{2}, 1\right)$
$\text{C.}$ $\left(0, \frac{\sqrt{2}}{2}\right]$
$\text{D.}$ $\left(0, \frac{1}{2}\right]$
设 $\mathrm{a}=2 \ln 1.01, \mathrm{~b}=\ln 1.02, \mathrm{c}=\sqrt{1.04}-1$, 则( )
$\text{A.}$ $a < b < c$
$\text{B.}$ $b < c < a$
$\text{C.}$ $ b < a < c $
$\text{D.}$ $ c < a < b$
填空题 (共 4 题 ),请把答案直接填写在答题纸上
已知双曲线 $C: \frac{x^{2}}{m}-y^{2}=1(m>0)$ 的一条渐近线为 $\sqrt{3} x+m y=0$, 则 $C$ 的焦距 为
已知向量 $\mathrm{a}=(1,3), \mathrm{b}=(3,4)$, 若 $\left(\mathrm{a}^{-} \lambda \mathrm{b}\right) \perp \mathrm{b}$, 则 $\lambda=$
记 $\triangle \mathrm{ABC}$ 的内角 $\mathrm{A}, \mathrm{B}, \mathrm{C}$ 的对边分别为 $\mathrm{a}, \mathrm{b}, \mathrm{c}$, 面积为 $\sqrt{3}, \mathrm{~B}=60^{\circ}, \mathrm{a}^{2}+\mathrm{c}^{2}=3 \mathrm{ac}$, 则 $b=$
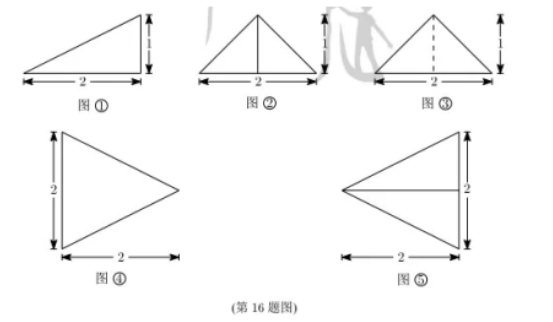
以图(1)为正视图和俯视图, 在图(2)(3)(4)(5)中选两个分别作为侧视图和俯视图, 组成某个三棱雉的三视图, 则所选侧视图和俯视图的编号依次为 (写 出符合要求的一组答案即可).
解答题 (共 7 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
某厂研究了一种生产高精产品的设备, 为检验新设备生产产品的某项指标有无提 高, 用一台旧设备和一台新设备各生产了 10 件产品, 得到各件产品该项指标数 据如下:
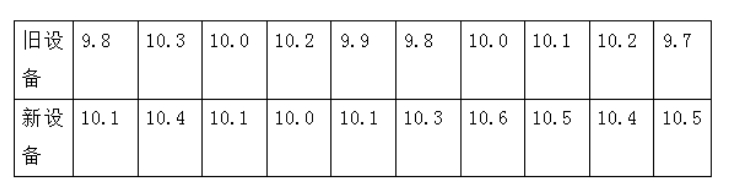
旧设备和新设备生产产品的该项指标的样本平均数分别记为和列, 样本方差分别 记为 $s_{1}^{2}$ 和 $s_{2}{ }^{2}$
(1)求 $\bar{x}, \bar{y}, \quad s_{1}^{2}, s_{2}^{2}$;
(2)判断新设备生产产品的该项指标的均值较旧设备是否有显著提高(如果 $\bar{y}-\bar{x} \geqslant 2 \sqrt{\frac{s_{1}^{2}+s_{2}^{2}}{2}}$, 则认为新设备生产产品的该项指标的均值较旧设备有显著 提高, 否则不认为有显著提高).
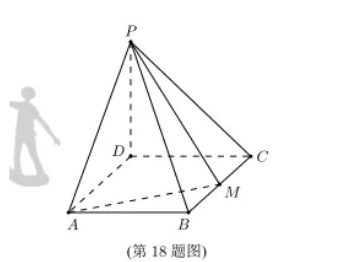
如图, 四棱雉 $P-A B C D$ 的底面是矩形, $P D \perp$ 底面 $A B C D, P D=D C=1, M$ 为 $B C$ 的中点, 且 $P B \perp A M$,
(1)求 $B C$;
(2)求二面角 $\mathrm{A}-\mathrm{PM}-\mathrm{B}$ 的正弦值。
记 $S_n$ 为数列 $\left\{a_{n}\right\}$ 的前 $n$ 项和, $b_{\mathrm{n}}$ 为数列 $\left\{S_{\mathrm{n}}\right\}$ 的前 $n$ 项积, 已知 $\frac{2}{s_{n}}+\frac{1}{b_{n}}=2$.
(1) 证明: 数列 $\left\{b_{n}\right\}$ 是等差数列;
(2)求 $\left\{\mathrm{a}_{n}\right\}$ 的通项公式.
设函数 $f(x)=\ln (a-x)$, 已知 $x=0$ 是函数 $y=x f(x)$ 的极值点。
(1)求 a;
(2)设函数 $g(x)=\frac{x+f(x)}{x f(x)}$, 证明: $g(x) < 1$.
己知抛物线 $C: \quad x^{2}=2 p y(p>0)$ 的焦点为 $F$, 且 $F$ 与圆 $M: x^{2}+(y+4)^{2}=1$ 上点的 距离的最小值为 $4 .$
(1)求 p;
(2)若点 $\mathrm{P}$ 在 $\mathrm{M}$ 上, $\mathrm{PA}, \mathrm{PB}$ 是 $\mathrm{C}$ 的两条切线, $\mathrm{A}, \mathrm{B}$ 是切点, 求 $\triangle \mathrm{PAB}$ 的最大值.
在直角坐标系 $x O y$ 中, $\odot C$ 的圆心为 $C(2,1)$, 半径为 1 .
(1) 写出 $\odot C$ 的一个参数方程; 的极坐标方程化为直角坐标方程;
(2)过点 $\mathrm{F}(4,1)$ 作 $\odot C$ 的两条切线, 以坐标原点为极点, $\mathrm{x}$ 轴正半轴为极轴 腱立极坐标系, 求这两条直线的极坐标方程.
已知函数 $f(x)=|x-a|+|x+3|$.
(1) 当 $\mathrm{a}=1$ 时, 求不等式 $\mathrm{f}(\mathrm{x}) \geqslant 6$ 的解集;
(2)若 $\mathrm{f}(\mathrm{x}) \geqslant-\mathrm{a}$, 求 $\mathrm{a}$ 的取值范围.