河北省衡水市部分学校2023-2024学年高三下学期二模考试数学试题

导出试卷

河北省衡水市部分学校2023-2024学年高三下学期二模考试数学试题

一、单选题（共 8 题），每题只有一个选项正确

1. 若

| a + b | = | a - b |, a = (1, 2), b = (m, 3)

, 则实数

m =

A.

B.

-6

C.

D.

-3

查看分享下载此题点赞(0) 收藏(1) 错题本(1) 白板加入试卷

2. 某中学举行数学解题比赛, 其中 5 人的比赛成绩分别为

70, 85, 90, 75, 95

, 则这 5 人成绩的上四分位数是

A.

B.

C.

D.

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

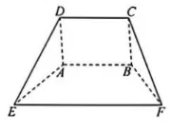
3. 生活中很多常见的工具有独特的几何体结构特征, 例如垃圾箕, 其结构如图所示的五面体

A D E - B C F

, 其中四边形

A B F E

与

C D E F

都为等腰梯形,

A B C D

为平行四边形. 若

A D ⊥

平面

A B F E

, 且

E F = 2 A B = 2 A E = 2 B F

, 记三棱锥体

D - A B F

的体积为

V_{1}

, 则该五面体的体积为

A.

3 V_{1}

B.

5 V_{1}

C.

4 V_{1}

D.

6 V_{1}

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

4. 已知

\tan α = 2

, 则

\frac{\sin 3 α}{\sin α + \cos α} =

A.

\frac{7}{9}

B.

\frac{2}{15}

C.

- \frac{7}{9}

D.

- \frac{2}{15}

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

5. 将 5 本不同的书 ( 2 本文学书、 2 本科学书和 1 本体育书) 分给甲、乙、丙三人, 每人至少分得 1 本书, 每本书只能分给一人，其中体育书只能分给甲、乙中的一人，则不同的分配方法数为

A.

B.

C.

100

D.

122

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

6. 已知

F_{1}, F_{2}

分别为双曲线

\frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}} = 1 (a) 0, b > 0)

的左、右焦点, 过.

F_{2}

与双曲线的一条渐近线平行的直线交双曲线于点

P

, 若

| P F_{1} | = 3 | P F_{2} |

, 则双曲线的离心率为

A.

B.

\sqrt{3}

C.

\sqrt{5}

D.

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

7. 已知函数

f (x), g (x)

的定义域为

R, g^{'} (x)

为

g (x)

的导函数, 且

f (x) + g^{'} (x) = 2, f (x) - g^{'}

(4 - x) = 2

. 若

g (x)

为偶函数, 则下列结论不一定成立的是

A.

f (4) = 2

B.

g^{'} (2) = 0

C.

f (- 1) = f (- 3)

D.

f (1) + f (3) = 4

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

8. 已知正数

a, b, c

满足

e^{a} = {1.1}^{3}, 5 b^{2} + 10 b - 3 = 0, e^{c} = 1.3

, 则

A.

a < c < b

B.

b < a < c

C.

c < a < b

D.

c < b < a

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

二、多选题（共 3 题），每题有多个选项正确

9. 已知

z \in C, z

: 是

z

的共轭复数, 则

A.

若

z = \frac{1 + 3 i}{1 - 3 i}

则

\bar{z} = \frac{- 4 - 3 i}{5}

B.

若

z

为纯虚数, 则

z^{2} < 0

C.

若

z^{-} (2 + i) > 0

, 则

z > 2 + i

D.

若

M = {z | | z + 3 i ∣⩽ 3}

, 则集合

M

所构成区域的面积为

6 π

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

10. 如图, 点 A, B, C 是函数.

f (x) = \sin (ω x + φ) (ω) 0)

的图象与直线

y = \frac{\sqrt{3}}{2}

相邻的三个交点,且

| B C | - | A B | = \frac{π}{3}, f (- \frac{π}{12}) = 0

, 则

A.

ω = 4

B.

函数

f (x)

在区间

((\frac{π}{3} \frac{π}{2})

上单调递减

C.

f (\frac{9 π}{8}) = \frac{1}{2}

D.

若将函数

f (x)

的图象沿

x

轴平移

θ

个单位, 得到一个偶函数的图象, 则

| θ |

的最小值为

\frac{π}{24}

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

11. 一个棱长为 4 的正四面体

P - ABC

容器,

D

是

PB

的中点,

E

是

CD

上的动点, 则

A.

直线

A E

与

P B

所成的角为

- \frac{π}{2}

B.

△ ABE

的周长最小值为

4 + \sqrt{34}

C.

若在这个容器中放入 1 个小球 (全部进入), 则小球的半径的最大值为

\frac{\sqrt{6}}{3}

D.

若在这个容器中放入 4 个完全相同的小球 (全部进入), 则小球半径的最大值为

\frac{2 \sqrt{6} - 2}{5}

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

三、填空题（共 3 题），请把答案直接填写在答题纸上

12. 设集合

A = {x ∣ x^{2} - 2 x - 3 < 0, x \in R}, B = {x | | x ∣> a, a > 0}

. 若

A \cup B = R

, 则实数

a

的取值范围为

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

13. 已知圆

x^{2} + y^{2} = 16

与直线

y = - \sqrt{3} x

交于

A, B

两点, 则经过点

A, B, C (8, 0)

的圆的方程为

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

14. 已知等差数列

{a_{n}}

(公差不为 0 ) 和等差数列

{b_{n}}

的前

n

项和分别为

S_{n}, T_{n}

, 如果关于

x

的实系数方程

1003 x^{2} - S_{1003} x + T_{1003} = 0

有实数解, 那么以下 1003 个方程

x^{2} - a_{i} x + b_{i} = 0 (i = 1, 2, \dots, 1003)

中, 有实数解的方程至少有 ________ 个.

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

四、解答题（共 5 题），解答过程应写出必要的文字说明、证明过程或演算步骤

15. 已知函数

f (x) = \frac{1}{2} - \sin^{2} ω x + \frac{\sqrt{3}}{2} \sin 2 ω x (ω) 0)

的最小正周期为

4 π

.
(1) 求

f (x)

在区问

[0, π]

上的单调递增区间;
(2) 在锐角

△ ABC

中, 内角

A, B, C

的对边分别是

a, b, c

, 满足

((2 a - c) \cos B = b \cdot \cos C

, 求函数

f (A)

的取值范围.

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

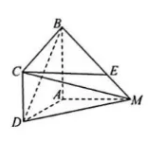
16. 如图, 在四棱锥

M - A B C D

中,

A B ⊥ A D, A B = A M = A D = 2, M B = 2 \sqrt{2}, M D = 2 \sqrt{3}

.
(1) 证明:

A B ⊥

平面

A D M

;
(2) 若

\vec{D C} = \frac{2}{3} \vec{A B}, \vec{B E} = 2 \vec{E M}

, 求直线

EC

与平面

BDM

所成角的正弦值.

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

17. 王老师每天早上 7: 00 准时从家里出发去学校, 他每天只会从地铁与汽车这两种交通工具中选择一个乘坐, 王老师多年积累的数据表明, 他到达学校的时间在这两种交通工具下的概率分布如下表所示:

(例如: 表格中 0.35 的含义是如果王老师当天乘地铁去学校, 则他到校时间在

7 : 35 - 7 : 40

的概率为 0.35 ).
(1) 某天早上王老师通过抛一枚质地均匀的硬币决定乘坐地铁还是乘坐汽车去学校, 若正面向上则坐地铁, 反面向上则坐汽车. 求他当天 7: 40-7: 45 到校的概率;

(2) 已知今天 (第一天) 王老师选择乘坐地铁去学校, 从第二天开始, 若前一天到校时间早于 7: 40 , 则当天他会乘坐地铁去学校, 否则当天他将乘坐汽车去学校. 且若他连续 10 天乘坐地铁, 则不论他前一天到校的时间是否早于 7: 40, 第 11 天他都将坐汽车到校. 记他从今天起 (包括今天) 到第一次乘坐汽车去学校前坐地铁的次数为

X

, 求

E (X)

;
(3) 已知今天 (第一天) 王老师选择乘坐地铁去学校. 从第二天开始, 若他前一天坐地铁去学校且到校时间早于 7: 40 , 则当天他会乘坐地铁去学校; 若他前一天坐地铁去学校且到校时间晚于 7: 40 , 则当天他会乘坐汽车去学校: 若他前一天乘坐汽车去学校, 则不论他前一天到校的时间是否早于 7: 40 , 当天他都会乘坐地铁去学校. 记

P n

为王老师第

n

天坐地铁去学校的概率, 求

P_{n}

的通项公式.

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

18. 已知

f (x) = a e^{2 x} - 2 x e^{x}

(其中

e = 2.71828

为自然对数的底数).
(1) 当

a = 0

时, 求曲线

y = f (x)

在点

(1, f (1))

处的切线方程;
(2) 当

a = \frac{1}{2}

时, 判断

y = f (x)

是否存在极值, 并说明理由;
(3)

\forall x \in R, f (x) + \frac{1}{a} \leq 0

, 求实数

a

的取值范围.

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

19. 圆、椭圆、双曲线都有对称中心, 统称为 “有心圆锥曲线”, 如下方式可以得到部分 “有心圆锥曲线”, 已知动点

P

与定点

A (m, 0)

的距离和

P

到定直线

x = \frac{n}{m}

的距离的比为常数

\frac{m}{n}

, 其中

m > 0, n > 0

, 且

m \neq n

, 记点

P

的轨迹为曲线

C

.
(1) 求曲线

C

的方程, 并说明轨迹的形状;
(2) 设点

B (- m, 0)

, 若曲线

C

上两动点

M, N

均在

x

轴上方,

A M ∥ B N

, 且

AN

与

BM

相交于点

Q

.
(i) 当

m = 2 \sqrt{2}, n = 4

时, 证明:

\frac{1}{| A M |} + \frac{1}{| B N |}

的值及

△ A B Q

的周长均为定值;
(ii) 当

m > n

时, 记

△ A B Q

的面积为

S

, 其内切圆半径为

r

, 试探究是否存在常数

λ

, 使得

S = λ r

恒成立? 若存在, 求

λ

(用

m, n

表示); 若不存在, 请说明理由.

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

非会员每天可以查看15道试题。开通会员，海量试题无限制查看。

无限看试题
下载试题
组卷

开通会员

热点推荐

试卷二维码

分享此二维码到群，让更多朋友参与

试卷白板

试卷白板提供了一个简单的触摸书写板，可供老师上课、或者视频直播时，直接利用白板给学生讲解试题，如有意见，欢迎反馈。