单选题 (共 6 题 ),每题只有一个选项正确
8 的相反数是
$\text{A.}$ $-8$
$\text{B.}$ 8
$\text{C.}$ $\frac{1}{8}$
$\text{D.}$ $-\frac{1}{8}$
下列运算正确的是()
$\text{A.}$ $a^{2}+a^{3}=a^{6}$
$\text{B.}$ $(a b)^{2}=a b^{2}$
$\text{C.}$ $(a+b)^{2}=a^{2}+b^{2}$
$\text{D.}$ $(a+b)(a-b)$
已知反比例函数 $y=\frac{k}{x}(k \neq 0)$, 且在各自象限内, $y$ 随 $x$ 的增大而增大, 则下列点可 能在这个函数图象上的为()
$\text{A.}$ $(2,3)$
$\text{B.}$ $(-2,3)$
$\text{C.}$ $(3,0)$
$\text{D.}$ $(-3,0)$
我们在外卖平台点单时会有点餐用的钱和外卖费 6 元, 我们计算了点单的总额和不
计算外卖费的总额的数据, 则两种情况计算出的数据一样的是()
$\text{A.}$ 平均数
$\text{B.}$ 中位数
$\text{C.}$ 众数
$\text{D.}$ 方差
下列说法正确的是()
$\text{A.}$ 命题一定有逆命题
$\text{B.}$ 所有的定理一定有逆定理
$\text{C.}$ 真命题的逆命题一定是真命题
$\text{D.}$ 假命题的逆命题一定是假命题
有一个正 $n$ 边形旋转 $90^{\circ}$ 后与自身重合, 则 $n$ 为 ( )
$\text{A.}$ 6
$\text{B.}$ 9
$\text{C.}$ 12
$\text{D.}$ 15
填空题 (共 12 题 ),请把答案直接填写在答题纸上
解方程组 $\left\{\begin{array}{l}x+y=1 \\ x^{2}-y^{2}=3\end{array}\right.$ 的结果为
已知 $x^2-2 \sqrt{3} x+m=0$ 有两个不相等的实数根, 则 $m$ 的取值范围是
甲、乙、丙三人参加活动, 两个人一组, 则分到甲和乙的概率为
某公司 5 月份的营业额为 25 万, 7 月份的营业额为 36 万, 已知 5 、 6 月的增长率 相同, 则增长率为
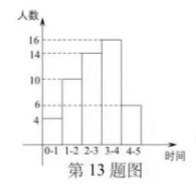
为了解学生的阅读情况, 对某校六年级部分学生的阅读情况展开调查, 并列出了相 应的频数分布直方图(如图所示)(每组数据含最小值, 不含最大值)(0-1 小时 4 人, 1-2 小时 10 人, 2-3 小时 14 人, 3-4 小时 16 人, 4-5 小时 6 人), 若共有 200 名学生, 则该学校六年级学生阅读时间不低于 3 小时的人数是
已知直线 $y=k x+b$ 过第一象限且函数值随着 $x$ 的增大而减小, 请列举出来这样的一 条直线:
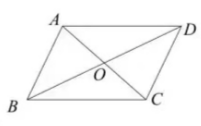
如图所示, 在口 $A B C D$ 中, $A C, B D$ 交于点 $O, \overrightarrow{B O}=\vec{a}, \overrightarrow{B C}=\vec{b}$, 则 $\overrightarrow{D C}=$
如图所示, 小区内有个圆形花坛 $O$, 点 $C$ 在弦 $A B$ 上, $A C=11, B C=21, O C=13$, 则这个花坛的面积为 . (结果保留 $\pi$ )
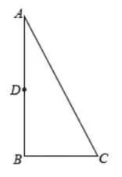
如图, 在 $\triangle A B C$ 中, $\angle A=30^{\circ}, \angle B=90^{\circ}, D$ 为 $A B$ 中点, $E$ 在线段 $A C$ 上, $\frac{A D}{A B}=\frac{D E}{B C}$,
则 $\frac{A E}{A C}=$
定义: 有一个圆分别和一个三角形的三条边各有两个交点, 截得的三条弦相等, 我 们把这个圆叫作“等弦圆", 现在有一个斜边长为 2 的等腰直角三角形, 当等弦圆最大时, 这个圆的半径为
解答题 (共 7 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
计算: $|-\sqrt{3}|-\left(\frac{1}{3}\right)^{-\frac{1}{2}}+\frac{2}{\sqrt{3}-1}-12^{\frac{1}{2}}$
解关于 $x$ 的不等式组 $\left\{\begin{array}{l}3 x>x-4 \\ \frac{4+x}{3}>x+2\end{array}\right.$
一个一次函数的截距为 1 , 且经过点 $A(2,3)$.
(1)求这个一次函数的解析式;
(2) 点 $A, B$ 在㭉个反比例函数上, 点 $B$ 横坐标为 6 , 将点 $B$ 向上平移 2 个单位得到点 $C$, 求 $\cos \angle A B C$ 的值.
我们经常会采用不同方法对某物体进行测量, 请测量下列灯杆 $A B$ 的长.
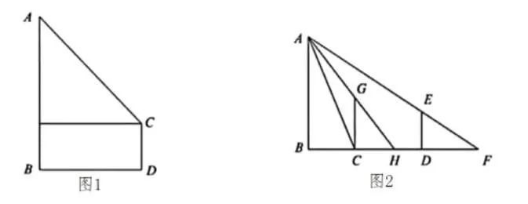
(1)如图 1 所示, 将一个澳角仪放置在距离灯杆 $A B$ 底部 $a$ 米的点 $D$ 处, 测角仪高为 $b$ 米, 从 $C$ 点测得 $A$ 点的仰角为 $\alpha$, 求灯杆 $A B$ 的高度. (用含 $a, b, a$ 的代数式表示)
(2)我国古代数学家赵爽利用影子对物体进行测量的方法, 在至今仍有借鉴意义图 2 所示, 现将一高度为 2 米的木杆 $C G$ 放在灯杆 $A B$ 前, 测得其影长 $C H$ 为 1 米, 再将木杆沿着 $B C$ 方向移动 $1.8$ 米至 $D E$ 的位置, 此时测得其影长 $D F$ 为 3 米, 求灯杆 $A B$ 的高度
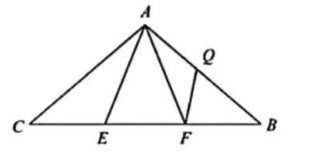
如图所示, 在等腰三角形 $A B C$ 中, $A B=A C$, 点 $E, F$ 在线段 $B C$ 上, 点 $Q$ 在线段 $A B$ 上, 且 $C F=B E, A E^{2}=A Q \cdot A B$ 求证:
(1) $\angle C A E=\angle B A F$;
(2) $C F \cdot F Q=A F \cdot B Q$
已知: $y=\frac{1}{2} x^{2}+b x+c$ 经过点 $A(-2,-1), B(0,-3)$.
(1)求函数解析式;
(2) 平移抛物线使得新顶点为 $P(m, n) \quad(m>0)$.
(1)倘若 $S_{\triangle O P B}=3$, 且在 $x=k$ 的右侧, 两抛物线都上升, 求 $k$ 的取值范围;
(2) $P$ 在原拋物线上, 新抛物线与 $y$ 轴交于 $Q, \angle B P Q=120^{\circ}$ 时, 求 $P$ 点坐标.
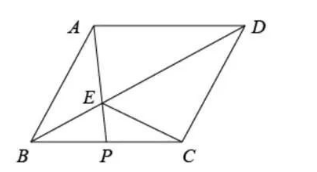
平行四边形 $A B C D$, 若 $P$ 为 $B C$ 中点, $A P$ 交 $B D$ 于点 $E$, 连接 $C E$.(1) 若 $A E=C E$,
(1)证明 $A B C D$ 为菱形;
(2) 若 $A B=5, A E=3$, 求 $B D$ 的长.
(2) 以 $\mathrm{A}$ 为圆心, $A E$ 为半径, $B$ 为圆心, $B E$ 为半径作圆, 两圆另一交点记为点 $F$, 且$C E=\sqrt{2} A E$. 若 $F$ 在直线 $C E$ 上, 求 $\frac{A B}{B C}$ 的值.