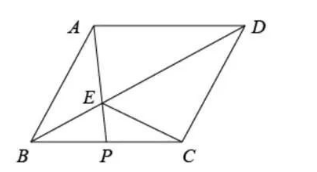
平行四边形 $A B C D$, 若 $P$ 为 $B C$ 中点, $A P$ 交 $B D$ 于点 $E$, 连接 $C E$.(1) 若 $A E=C E$,
(1)证明 $A B C D$ 为菱形;
(2) 若 $A B=5, A E=3$, 求 $B D$ 的长.
(2) 以 $\mathrm{A}$ 为圆心, $A E$ 为半径, $B$ 为圆心, $B E$ 为半径作圆, 两圆另一交点记为点 $F$, 且$C E=\sqrt{2} A E$. 若 $F$ 在直线 $C E$ 上, 求 $\frac{A B}{B C}$ 的值.