2024年1月普通高等学校招生全国统一考试适应性测试（九省联考）数学试题

导出试卷

2024年1月普通高等学校招生全国统一考试适应性测试（九省联考）数学试题

一、单选题（共 8 题），每题只有一个选项正确

1. 样本数据

16, 24, 14, 10, 20, 30, 12, 14, 40

的中位数为

A.

B.

C.

D.

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

2. 椭圆

\frac{x^{2}}{a^{2}} + y^{2} = 1 (a > 1)

的离心率为

\frac{1}{2}

, 则

a =

A.

\frac{2 \sqrt{3}}{3}

B.

\sqrt{2}

C.

\sqrt{3}

D.

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

3. 记等差数列

{a_{n}}

的前

n

项和为

S_{n}, a_{3} + a_{7} = 6, a_{12} = 17

, 则

S_{16} =

A.

120

B.

140

C.

160

D.

180

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

4. 设

α, β

是两个平面,

m, l

是两条直线, 则下列命题为真命题的是

A.

若

α ⊥ β, m / / α, l / / β

, 则

m ⊥ l

B.

若

m \subset α, l \subset β, m / / l

, 则

α / / β

C.

若

α \cap β = m, l / / α, l / / β

, 则

m / / l

D.

若

m ⊥ α, l ⊥ β, m / / l

, 则

α ⊥ β

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

5. 甲、乙、丙等 5 人站成一排, 且甲不在两端, 乙和丙之间恰有 2 人, 则不同排法共有

A.

20 种

B.

16 种

C.

12 种

D.

8 种

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

6. 已知

Q

为直线

l : x + 2 y + 1 = 0

上的动点, 点

P

满足

\overset{―}{Q P} = (1, - 3)

, 记

P

的轨迹为

E

, 则

A.

E

是一个半径为

\sqrt{5}

的圆

B.

E

是一条与

l

相交的直线

C.

E

上的点到

l

的距离均为

\sqrt{5}

D.

E

是两条平行直线

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

7. 已知

θ \in (\frac{3 π}{4}, π), \tan 2 θ = - 4 \tan (θ + \frac{π}{4})

, 则

\frac{1 + \sin 2 θ}{2 \cos^{2} θ + \sin 2 θ} =

A.

\frac{1}{4}

B.

\frac{3}{4}

C.

D.

\frac{3}{2}

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

8. 设双曲线

C : \frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}} = 1 (a > 0, b > 0)

的左、右焦点分别为

F_{1}, F_{2}

，过坐标原点的直线与

C

交于

A, B

两点,

| F_{1} B | = 2 | F_{1} A |, \overset{―}{F_{2} A} \cdot \overset{―}{F_{2} B} = 4 a^{2}

, 则

C

的离心率为

A.

\sqrt{2}

B.

C.

\sqrt{5}

D.

\sqrt{7}

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

二、多选题（共 3 题），每题有多个选项正确

9. 已知函数

f (x) = \sin (2 x + \frac{3 π}{4}) + \cos (2 x + \frac{3 π}{4})

, 则

A.

函数

f (x - \frac{π}{4})

为偶函数

B.

曲线

y = f (x)

的对称轴为

x = k π, k \in Z

C.

f (x)

在区间

(\frac{π}{3}, \frac{π}{2})

单调递增

D.

f (x)

的最小值为 -2

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

10. 已知复数

z, w

均不为 0 , 则

A.

z^{2} = | z |^{2}

B.

\frac{z}{\bar{z}} = \frac{z^{2}}{| z |^{2}}

C.

\overset{―}{z - w} = \bar{z} - \bar{w}

D.

| \frac{z}{w} | = \frac{| z |}{| w |}

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

11. 已知函数

f (x)

的定义域为

R

, 且

f (\frac{1}{2}) \neq 0

, 若

f (x + y) + f (x) f (y) = 4 x y

, 则

A.

f (- \frac{1}{2}) = 0

B.

f (\frac{1}{2}) = - 2

C.

函数

f (x - \frac{1}{2})

是偶函数

D.

函数

f (x + \frac{1}{2})

是减函数

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

三、填空题（共 3 题），请把答案直接填写在答题纸上

12. 已知集合

A = {- 2, 0, 2, 4}, B = {x | | x - 3 ∣⩽ m}

, 若

A \cap B = A

, 则

m

的最小值为

查看分享下载此题点赞(1) 收藏(0) 错题本(0) 白板加入试卷

13. 已知轴截而为正三角形的圆锥

M M^{'}

的高与球

O

的直径相等, 则圆锥

M M^{'}

的体积与球

O

的体积的比值是是 ________ ，圆锥

M M^{'}

的表面积与球

O

的表面积的比值是 ________

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

14. 以

max M

表示数集

M

中报大的数. 设

0 < a < b < c < 1

, 已知

b ⩾ 2 a

或

a + b ⩽ 1

, 则

max {b - a, c - b, 1 - c}

的最小值为

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

四、解答题（共 5 题），解答过程应写出必要的文字说明、证明过程或演算步骤

15. 已知函数

f (x) = \ln x + x^{2} + \infty x + 2

在点

(2, f (2))

处的切线与直线

2 x + 3 y = 0

垂直.
(1) 求

a

;
(2) 求

f (x)

的单调区间和极值.

查看分享下载此题点赞(1) 收藏(0) 错题本(0) 白板加入试卷

16. 盒中有标记数字

1, 2, 3, 4

的小球各 2 个, 随机一次取出 3 个小球.
(1) 求取出的 3 个小球上的数字两两不同的概率;
(2) 记取出的 3 个小球上的最小数字为

X

, 求

X

的分布列及数学期望

E (X)

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

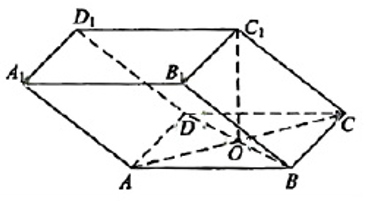
17. 如图, 平行六面体

A B C D - A_{1} B_{1} C_{1} D_{1}

中, 底面

A B C D

是边长为 2 的正方形,

O

为

A C

与

B D

的交点,

A A_{1} = 2, ∠ C_{1} C B ≅ ∠ C_{1} C D, ∠ C_{1} C O = 45^{\circ}

.
(1) 证明:

C_{1} O ⊥

平面

A B C D

;
(2) 求二面角

B - A A_{1} - D

的正弦值.

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

18. 已知拋物线

C : y^{2} = 4 x

的焦点为

F

, 过

F

的直线

l

交

C

于

A, B

两点, 过

F

与

l

垂直的直线交

C

手

D, E

两点, 其中

B, D

在

x

轴上方,

M, N

分别为

A B, D E

的中点.
(1) 证明：直线

M N

过定点;
(2) 设

G

为直线

A E

与直线

B D

的交点, 求

△ G M N

面积的最小值.

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

19. 离散对数在密码学中有重要的应用. 设

p

是素数，集合

X = {1, 2, \dots, p - 1}

, 若

u, v \in X ， m \in N

，记

u \otimes v

为

u v

除以

p

的余数，

u^{m, \otimes}

为

u^{m}

除以

p

的余数；设

a \in X

，

1, a, a^{2 . \otimes}, \dots, a^{p - 2, \otimes}

两两不同, 若

a^{n, \oplus} = b (n \in {0, 1, \dots, p - 2})

, 则称

n

是以

a

为底

b

的离散对数, 记为

n = \log (p)_{a} b

.
(1) 若

p = 11, a = 2

, 求

a^{p - 1, \otimes}

;
(2) 对

m_{1}, m_{2} \in {0, 1, \dots, p - 2}

, 记

m_{1} \oplus m_{2}

为

m_{1} + m_{2}

除以

p - 1

的余数 (当

m_{1} + m_{2}

能被

p - 1

整除时,

m_{1} \oplus m_{2} = 0

). 证明:

\log (p)_{0} (b \otimes c) = \log (p)_{0} b \oplus \log (p)_{0} c

, 其中

b, c \in X

;
(3) 已知

n = \log (p)_{a} b

. 对

x \in X, k \in {1, 2, \dots, p - 2}

, 令

y_{1} = a^{k, θ}, y_{2} = x \otimes b^{k, θ}

. 证明:

x = y_{2} \otimes y_{1}^{n (p - 2 λ \otimes}

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

非会员每天可以查看15道试题。开通会员，海量试题无限制查看。

无限看试题
下载试题
组卷

开通会员

热点推荐

试卷二维码

分享此二维码到群，让更多朋友参与

试卷白板

试卷白板提供了一个简单的触摸书写板，可供老师上课、或者视频直播时，直接利用白板给学生讲解试题，如有意见，欢迎反馈。