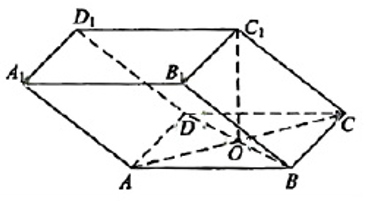
如图, 平行六面体 $A B C D-A_1 B_1 C_1 D_1$ 中, 底面 $A B C D$ 是边长为 2 的正方形, $O$ 为 $A C$与 $B D$ 的交点, $A A_1=2, \angle C_1 C B \cong \angle C_1 C D, \angle C_1 C O=45^{\circ}$.
(1) 证明: $C_1 O \perp$ 平面 $A B C D$;
(2) 求二面角 $B-A A_1-D$ 的正弦值.
(1) 证明: $C_1 O \perp$ 平面 $A B C D$;
(2) 求二面角 $B-A A_1-D$ 的正弦值.
