单选题 (共 8 题 ),每题只有一个选项正确
设集合 $A=\{x \mid 1 < x < 4\}$, 集合 $B=\left\{x \mid x^{2}-2 x-3 \leqslant 0\right\}$, 则 $A \cap B=$
$\text{A.}$ $[-1,4)$
$\text{B.}$ $(-1,4)$
$\text{C.}$ $(1,3]$
$\text{D.}$ $(1,3)$
已知函数 $f(x)$ 在 $\mathbf{R}$ 上是单调函数, 且满足对任意 $x \in \mathrm{R}$, 都有 $f\left[f(x)-2^{x}\right]=3$, 则 $f(3)$ 的值是
$\text{A.}$ 3
$\text{B.}$ 7
$\text{C.}$ 9
$\text{D.}$ 12
已知 $a=3^{0.2}, b=\log _{6} 7, c=\log _{5} 6$, 则
$\text{A.}$ $a>b>c$
$\text{B.}$ $b>c>a$
$\text{C.}$ $a>c>b$
$\text{D.}$ $b>a>c$
在数列 $\left\{a_{n}\right\}$ 中, $a_{1}=2, a_{n+1}=a_{n}+\ln \left(1+\frac{1}{n}\right)$, 则 $a_{n}=$
$\text{A.}$ $2+\ln n$
$\text{B.}$ $2+(n-1) \ln n$
$\text{C.}$ $2+n \ln n$
$\text{D.}$ $1+n+\ln n$
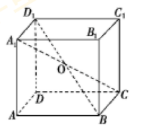
如图, 已知正方体 $A B C D-A_{1} B_{1} C_{1} D_{1}$ 的中心为 $O$, 则下列结论中
1. $\overrightarrow{O A}+\overrightarrow{O D}$ 与 $\overrightarrow{O A}_{1}+\overrightarrow{O D}_{1}$ 是一对相反向量;
2.$\overrightarrow{O B}-\overrightarrow{O C}_{1}$ 与 $\overrightarrow{O C}-\overrightarrow{O B}_{1}$ 是一对相反向量;
3.$\overrightarrow{O A}_{1}+\overrightarrow{O B}_{1}+\overrightarrow{O C}_{1}+\overrightarrow{O D}_{1}$ 与 $\overrightarrow{O D}+\overrightarrow{O C}+\overrightarrow{O B}+\overrightarrow{O A}$ 是一对相反向量;
4.$\overrightarrow{O C}-\overrightarrow{O A}$ 与 $\overrightarrow{O C}_{1}-\overrightarrow{O A}_{1}$ 是一对相反向量.
正确结论的个数为
$\text{A.}$ 1
$\text{B.}$ 2
$\text{C.}$ 3
$\text{D.}$ 4
“ $k < 2$ ”是“方程 $\frac{x^{2}}{25-k}+\frac{y^{2}}{k-9}=1$ 表示双曲线”的
$\text{A.}$ 充分不必要条件
$\text{B.}$ 必要不充分条件
$\text{C.}$ 充要条件
$\text{D.}$ 既不充分也不必要条件
已知函数 $f(x)=a \ln x-b x^{2}$ 的图象在 $x=1$ 处与直线 $y=-\frac{1}{2}$ 相切, 则函数 $f(x)$ 在 $[1, \mathrm{e}]$ 上的最大值为
$\text{A.}$ $-1$
$\text{B.}$ 0
$\text{C.}$ $-\frac{1}{2}$
$\text{D.}$ 1
已知平面向量 $\vec{a}, \vec{b}, \vec{c}$ 满足 $|\vec{a}|=|\vec{b}|=\vec{a} \cdot \vec{b}=2$, 且 $(\vec{b}-\vec{c}) \cdot(3 \vec{b}-\vec{c})=0$, 则 $|\vec{c}-\vec{a}|$ 最小值 为
$\text{A.}$ $2 \sqrt{2}+1$
$\text{B.}$ $3 \sqrt{3}-3$
$\text{C.}$ $\sqrt{7}-1$
$\text{D.}$ $2 \sqrt{3}-2$
多选题 (共 4 题 ),每题有多个选项正确
若 $0 < a < b$, 且 $a^{2}+b^{2}=2$, 则
$\text{A.}$ $1 < b < \sqrt{2}$
$\text{B.}$ $b-a>1$
$\text{C.}$ $a b+a+b \leqslant 3$
$\text{D.}$ $a^{3}+b^{3} \geqslant 2$
中国古代数学著作《算法统综》中有这样一个问题: “三百七十八里关, 初步健步不为 难, 次日脚痛减一半, 六朝才得到其关, 要见次日行里数, 请公仔仔细算相还”. 其大意 为: “有一人走 378 里路, 第一天健步行走, 从第二天起脚痛每天走的路程为前一天的 一半, 走了 6 天后到达目的地”. 则下列说法正确的是
$\text{A.}$ 该人第五天走的路程为 12 里
$\text{B.}$ 该人第三天走的路程为 42 里
$\text{C.}$ 该人前三天共走的路程为 330 里
$\text{D.}$ 该人最后三天共走的路程为 42 里
设 $\vec{a}$ 与 $\vec{b}$ 是两个不共线向量, 关于向量 $\vec{a}+\lambda \vec{b},(\lambda-1) \vec{a}+2 \lambda \vec{b},-(\vec{b}-2 \vec{a})$, 则下列结论中 正确的是
$\text{A.}$ 当 $\lambda>1$ 时, 向量 $\vec{a}+\lambda \vec{b},(\lambda-1) \vec{a}+2 \lambda \vec{b}$ 不可能共线
$\text{B.}$ 当 $\lambda>-3$ 时, 向量 $\vec{a}+\lambda \vec{b},-(\vec{b}-2 \vec{a})$ 可能出现共线情况
$\text{C.}$ 若 $\vec{a} \cdot \vec{b}=0$, 且 $\vec{a}, \vec{b}$ 为单位向量, 则当 $\lambda>-3$ 时, 向量 $(\lambda-1) \vec{a}+2 \lambda \vec{b},-(\vec{b}-2 \vec{a})$ 可能 出现垂直情况
$\text{D.}$ 当 $\lambda=2$ 时, 向量 $\vec{a}-\lambda \vec{b}$ 与 $-2(2 \vec{b}-\vec{a})$ 平行
已知函数 $f(x)=|x-2|+1, g(x)=k x$, 若方程 $f(x)=g(x)$ 有两个不相等的实根, 则实数 $k$ 的取值可以是
$\text{A.}$ $\frac{4}{3}$
$\text{B.}$ $\frac{3}{4}$
$\text{C.}$ $\frac{4}{5}$
$\text{D.}$ 1
填空题 (共 6 题 ),请把答案直接填写在答题纸上
$(x-5 a)^{10}$ 的展开式中, $x^{7}$ 的系数为 15 , 则 $a=$
在 $\triangle A B C$ 中, $\angle A=45^{\circ}, \angle C=105^{\circ}, B C=6 \sqrt{2}$, 则 $A C$ 的长度为
一只红铃虫产卵数 $y$ 和温度 $x$ 有关, 现测得一组数据 $\left(x_{i}, y_{i}\right)(\mathrm{i}=1,2, \cdots, 10)$, 可用模型 $y$ $300, y_{1} y_{2} \cdots y_{10}=\mathrm{e}^{50}$, e 为自然常数, 则 $c_{1} c_{2}=$
已知矩形 $A B C D$ 的周长为 18 , 把它沿图中的虚线折成正六棱柱, 当这个正六棱柱的 体积最大时, 它的外接球的表面积为

某寻宝游戏的棋盘路线图上, 依次标有起点 第 1 站 第 2 站 $\cdots$ 第 20 站, 选手通过抛 郑均匀硬币, 从起点 (不同于第 1 站) 依序向第 1 站 第 2 站 $\cdots$ 第 20 站前进:若掷出正 面, 棋子从所在站点前进到下 1 站停留; 若掷出反面, 棋子则从所在站点连续前进 2 站 停留, 直到到达第 19 站或第 20 站, 游戏结束, 设游戏过程中棋子停留在第 $n(n=1,2$, $\cdots, 20)$ 站的概率为 $P_{n}$.
(1) 从游戏开始计算, 若抛郑均匀硬币 3 次后棋子停留在第 $X$ 站, 求 $X$ 的分布列与数学 期望;
(2) 甲乙两人约定 : 由裁判员通过不断拋掷硬币, 让棋子从起点出发, 并按上述规则依 序前进, 直到游戏结束. 若棋子最终停留性第 19 站, 则甲选手获胜; 若棋子最终停留在 第 20 站, 则乙选手获胜. 试分析这个约定对甲乙两人是否公平.
已知等差数列 $\left\{a_{n}\right\}$ 的前 $n$ 项和为 $S_{n}, a_{1}+a_{5}=10, S_{9}=81$.
(1) 求 $a_{n}$;
(2) 若集合 $A=\left\{x \mid x=a_{n}, n \in N^{*}\right\}, B=\left\{x \mid x=2^{n}, n \in N^{*}\right\}$, 将 $A \cup B$ 中的所有元素按从 小到大顺序排列, 构成数列 $\left\{b_{n}\right\}$. 设数列 $\left\{b_{n}\right\}$ 的前 $n$ 项和为 $T_{n}$, 求 $T_{33}$.
解答题 (共 4 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
已知向量 $\vec{a}=\left(\sin x, \frac{3}{4}\right), \vec{b}=(\cos x,-1)$.
(1) 当 $\vec{a} / / \vec{b}$ 时, 求 $\cos ^{2} x-\sin 2 x$ 的值;
(2) 设函数 $f(x)=2(\vec{a}+\vec{b}) \cdot \vec{b}$, 已知在 $\triangle A B C$ 中, 内角 $A 、 B 、 C$ 的对边分别为 $a, b, c$, 若 $a=\sqrt{3}, b=2, \sin B=\frac{\sqrt{6}}{3}$, 求 $f(x)+4 \cos \left(2 A+\frac{\pi}{6}\right)\left(x \in\left[0, \frac{\pi}{3}\right]\right)$ 的取值范围.
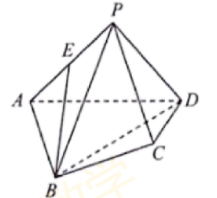
18. 如图, 在四棱锥 $P-A B C D$ 中, $A B=B D=B P=\sqrt{5}, P A=P D=\sqrt{2}, \angle A P D=90^{\circ}, E$ 是棱 $P A$ 的中点, 且 $B E / /$ 平面 $P C D$.
(1) 证明: $C D \perp$ 平面 $P A D$;
(2) 若 $C D=1$, 求二面角 $A-P B-C$ 的余弦值.
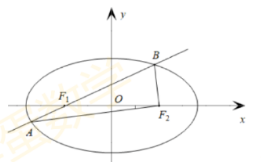
如图, 椭圆 $E: \frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1(a>b>0)$ 的左焦点为 $F_{1}$, 右焦点为 $F_{2}$, 离心率 $\mathrm{e}=\frac{1}{2}$, 过 $F_{1}$ 的直线交椭圆于 $A 、 B$ 两点, 且 $\triangle A B F_{2}$ 的周长为 8 .
(1) 求椭圆 $E$ 的方程;
(2) 设动直线 $l: y=k x+m$ 与椭圆 $E$ 有且只有一个公共点 $P$, 且与直线 $x=4$ 相交于点 $Q$, 试探究: 在 $x$ 轴上是否存在定点 $M$, 使得以 $P Q$ 为直径的圆恒过点 $M$ ? 若存在, 求 出点 $M$ 的坐标; 若不存在, 说明理由.
已知函数 $f(x)=\ln x, g(x)=a x^{2}-2 a x(a \neq 0)$.
(1) 若 $a=3$, 判断函数 $y=f(x)-g(x)$ 的单调性;
(2) 若函数 $h(x)=f(x)+g(x)$ 的导函数 $h^{\prime}(x)$ 有两个零点 $x_{1}, x_{2}\left(x_{1} < x_{2}\right)$, 证明: $h\left(x_{2}\right)-h$ $\left(x_{1}\right)>f(2 a)+g(1)$.