单选题 (共 11 题 ),每题只有一个选项正确
. 已知集合 $A=\{1,2,4\}$, 集合 $B=\{a, a+2\}$, 若 $A \cap B=B$, 则 $a=$
$\text{A.}$ 0
$\text{B.}$ $\frac{1}{2}$
$\text{C.}$ 1
$\text{D.}$ 2
命题: $\mathrm{p}: \forall x \in \mathrm{R}, x+|x| \geq 0$ 的否定为
$\text{A.}$ $\exists x \in \mathrm{R}, x+|x| \geq 0$
$\text{B.}$ $\exists x \in R, x+|x| \leq 0$
$\text{C.}$ $\exists x \in \mathrm{R}, x+|x| < 0$
$\text{D.}$ $\forall x \in \mathrm{R}, x+|x| < 0$
下列函数为奇函数且在 $(0,1)$ 上为减函数的是
$\text{A.}$ $f(x)=\sin (-x)$
$\text{B.}$ $f(x)=\tan x$
$\text{C.}$ $f(x)=\cos x$
$\text{D.}$ $f(x)=\sin x$
设 $a, b$ 为实数, 则“ $a < b < 0$ ”是 $=\frac{1}{a} < \frac{1}{b}$ ”的
$\text{A.}$ 充分而不必要条件
$\text{B.}$ 必要而不充分条件
$\text{C.}$ 充分必要条件
$\text{D.}$ 既不充分也不必要条件
若不等式 $m x^2+m x-4 < 2 x^2+2 x-1$ 对任意实数 $\mathrm{x}$ 均成立, 则实数 $\mathrm{m}$ 的取值范围是
$\text{A.}$ $(-2,2)$
$\text{B.}$ $(-10,2]$
$\text{C.}$ $(-\infty,-2) \cup[2,+\infty)$
$\text{D.}$ $(-\infty,-2]$
已知 $f(x)=\sin \left(\frac{\pi}{3} x+\frac{\pi}{3}\right)-\sqrt{3} \cos \left(\frac{\pi}{3} x+\frac{\pi}{3}\right)$, 则 $f(1)+f(2)+\cdots+f(2023)$ 的值为
$\text{A.}$ $2 \sqrt{3}$
$\text{B.}$ $\sqrt{3}$
$\text{C.}$ 1
$\text{D.}$ 0
已知 $\triangle A B C$ 中, $A C=2, \sin A=\tan B, A \in\left(0, \frac{\pi}{3}\right]$, 则边 $A B$ 的最小值为
$\text{A.}$ 2
$\text{B.}$ 3
$\text{C.}$ $2+\sqrt{3}$
$\text{D.}$ $\frac{5}{2}$
已知 $a=1.4, b=1.1 \mathrm{e}^{0.4}, c=\mathrm{e}^{0.5}$, 则 $a, b, c$ 的大小关系是
$\text{A.}$ $a < b < c$
$\text{B.}$ $a < c < b$
$\text{C.}$ $b < c < a$
$\text{D.}$ $c < b < a$
已知实数 $a, b$ 满足等式 $\left(\frac{1}{2}\right)^a=\left(\frac{1}{3}\right)^b$, 则下列不可能成立的有
$\text{A.}$ $a=b$
$\text{B.}$ $0>b>a$
$\text{C.}$ $b>a>0$
$\text{D.}$ $0>a>b$
计算下列各式, 结果为 $\sqrt{3}$ 的是
$\text{A.}$ $\sqrt{2} \sin 15^{\circ}+\sqrt{2} \cos 15^{\circ}$
$\text{B.}$ $\cos ^2 15^{\circ}-\sin 15^{\circ} \cos 75^{\circ}$
$\text{C.}$ $\frac{\tan 15^{\circ}}{1-\tan ^2 15^{\circ}}$
$\text{D.}$ $\frac{1+\tan 15^{\circ}}{1-\tan 15^{\circ}}$
已知函数 $f(x)$ 定义域为 $\mathrm{R}, f(x+1)$ 是奇函数, $g(x)=(1-x) f(x)$, 函数 $g(x)$ 在 $[1,+\infty)$ 上递增, 则 下列命题为真命题的是
$\text{A.}$ $f(-x-1)=-f(x+1)$
$\text{B.}$ 函数 $g(x)$ 在 $(-\infty, 1]$ 上递减
$\text{C.}$ 若 $a < 2-b < 1$, 则 $g(1) < g(b) < g(a)$
$\text{D.}$ 若 $g(a)>g(a+1)$, 则 $a < \frac{1}{2}$
多选题 (共 1 题 ),每题有多个选项正确
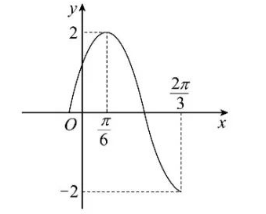
已知函数 $f(x)=A \cos (\omega x+\varphi)\left(A>0, \omega>0,|\varphi| < \frac{\pi}{2}\right)$ 的部分图像如图所示, 将 $f(x)$ 的图像向左平移 $\frac{\pi}{4}$ 个 单位长度, 再向上平移 1 个单位长度后得到函数 $g(x)$ 的图像, 则
$\text{A.}$ $f(x)=2 \cos \left(2 x-\frac{\pi}{3}\right)$
$\text{B.}$ $g(x)=2 \cos \left(2 x+\frac{\pi}{6}\right)+1$
$\text{C.}$ $g(x)$ 的图像关于点 $\left(\frac{\pi}{6}, 0\right)$ 对称
$\text{D.}$ $g(x)$ 在 $\left[-\frac{\pi}{12}+k \pi, \frac{5 \pi}{12}+k \pi\right](k \in \mathrm{Z})$ 上单调递减
填空题 (共 4 题 ),请把答案直接填写在答题纸上
扇形的圆心角为 $60^{\circ}$, 半径为 4 , 则扇形的面积为
已知 $f(x)$ 是定义域为 $\mathbf{R}$ 的奇函数, 当 $x>0$ 时, $f(x)=\log _5 x+1$, 则 $f(-5)=$
已知函数 $f(x)=\cos \left(\omega x-\frac{\pi}{6}\right)(\omega>0)$ 在区间 $\left(\frac{7 \pi}{6 \omega}, 2 \pi\right]$ 上有且只有 2 个零点, 则 $\omega$ 的取值范围 是
已知 $a>\frac{1}{2}, b>\frac{1}{3}, \frac{1}{a}+\frac{2}{b}=7$, 则 $\frac{3}{2 a-1}+\frac{1}{3 b-1}$ 的最小值
解答题 (共 6 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
$\triangle A B C$ 中, 角 $A, B, C$ 所对应的边分别为 $a, b, c$, 且 $\sqrt{3} a \cos B=2 c \sin A-\sqrt{3} b \cos A$.
(I) 求角 $\mathrm{A}$ 的大小;
(II) 若 $\triangle A B C$ 的面积为 $4 \sqrt{3}, a$ 是 $b, c$ 的等差中项, 求 $\triangle A B C$ 的周长.
已知数列 $\left\{a_n\right\}$ 是递增的等比数列, 且 $a_2+a_3=12, a_1 \cdot a_4=27$.
( I) 求数列 $\left\{a_n\right\}$ 的通项公式;
(II) 设 $S_n$ 为数列 $\left\{a_n\right\}$ 的前 $n$ 项和, $b_n=\frac{a_{n+1}}{S_n S_{n+1}}$, 求数列 $\left\{b_n\right\}$ 的前 $n$ 项和 $T_n$.
如图, 在四棱椎 $P-A B C D$ 中, $P A \perp$ 平面 $A B C D, A B / / C D, A B \perp A D, A B=1, P A=A D=C D=2, E$ 为棱 $P C$ 上一点, 平面 $A B E$ 与棱 $P D$ 交于点 $F$. 且 $B E \perp P C$.
(I) 求证: $F$ 为 $P D$ 的中点;
(II) 求二面角 $B-F C-P$ 的余弦值.
某公司是一家集无人机特种装备的研发、制造与技术服务的综合型科技创新企业. 该公司生产的甲、乙两 种类型无人运输机性能都比较出色, 但操控水平需要十分姆熟, 才能发挥更大的作用. 已知在单位时间内, 甲、乙两种类型的无人运输机操作成功的概率分别为 $\frac{2}{3}$ 和 $\frac{1}{2}$, 假设每次操作能否成功相互独立.
(I) 该公司分别收集了甲型无人运输机在 5 个不同的地点测试的两项指标数 $x_i, y_i(i=1,2,3,4,5)$, 数 据如下表所示:

试求 $y$ 与 $x$ 间的相关系数 $r$, 并利用 $r$ 说明 $y$ 与 $x$ 是否具有较强的线性相关关系; (若 $\mid r>0.75$, 则线性相关 程度很高)
(II) 操作员连续进行两次无人机的操作有两种方案:
方案一: 在初次操作时, 随机选择两种无人运输机中的一种, 若初次操作成功, 则第二次继续使用该类型 设备; 若初次操作不成功, 则第二次使用另一类型进行操作.
方案二: 在初次操作时, 随机选择两种无人运输机中的一种, 无论初次操作是否成功, 第二次均使用初次 所选择的无人运输机进行操作.
假定方案选择及操作不相互影响, 试比较这两种方案的操作成功的次数的期望值.
附:参考公式及数据: $r=\frac{\sum_{i=1}^n\left(x_i-\bar{x}\right)\left(y_i-\bar{y}\right)}{\sqrt{\sum_{i=1}^n\left(x_i-\bar{x}\right)^2} \sqrt{\sum_{i=1}^n\left(y_i-\bar{y}\right)^2}}$.
已知曲线 $\mathrm{E}$ 上任意一点 $\mathrm{Q}$ 到定点 $F(\sqrt{14}, 0)$ 的距离与 $\mathrm{Q}$ 到定直线 $m: x=\frac{9 \sqrt{14}}{14}$ 的距离之比为 $\frac{\sqrt{14}}{3}$.
(I) 求曲线 $\mathrm{E}$ 的轨迹方程:
(II) 斜率为 $k\left(k>\frac{\sqrt{5}}{3}\right)$ 的直线 1 交曲线 $\mathrm{E}$ 于 $\mathrm{B}, \mathrm{C}$ 两点, 线段 $\mathrm{BC}$ 的中点为 $\mathrm{M}$, 点 $\mathrm{M}$ 在 $\mathrm{x}$ 轴下方, 直线 $O M$ 交曲线 $\mathrm{E}$ 于点 $\mathrm{N}$, 交直线 $x=-1$ 于点 $\mathrm{D}$, 且满足 $|O N|^2=|O D \| O M|$ (O 为原点). 求证: 直线 1 过定点.
已知函数 $f(x)=x+\frac{a}{\mathrm{e}^x}(a>0)$.
(I) 求函数 $f(x)$ 的极值;
(II) 若函数 $f(x)$ 有两个不相等的零点 $x_1, x_2$,
(i) 求 $a$ 的取值范围;
(ii) 证明: $x_1+x_2>2 \ln a$.