单选题 （共 10 题 ），每题只有一个选项正确
-5 的相反数是
$\text{A.}$ 5
$\text{B.}$ -5
$\text{C.}$ $\frac{1}{5}$
$\text{D.}$ $-\frac{1}{5}$
下列计算正确的是
$\text{A.}$ $a^4+a^4=a^8$
$\text{B.}$ $a^4 \cdot a^4=a^{16}$
$\text{C.}$ $\left(a^4\right)^4=a^{16}$
$\text{D.}$ $a^8 \div a^4=a^2$
在数轴上表示不等式 $\frac{x-1}{2} < 0$ 的解集, 正确的是
$\text{A.}$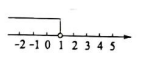 
$\text{B.}$ 
$\text{C.}$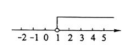 
$\text{D.}$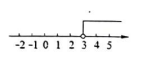 
下列函数中, $y$ 的值随 $x$ 值的增大而减小的是
$\text{A.}$ $y=x^2+1$
$\text{B.}$ $y=-x^2+1$
$\text{C.}$ $y=2 x+1$
$\text{D.}$ $y=-2 x+1$
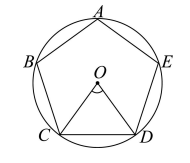
如图, 正五边形 $A B C D E$ 内接于 $\odot O$, 连接 $O C, O D$, 则 $\angle B A E-\angle C O D=$
$\text{A.}$ $60^{\circ}$
$\text{B.}$ $54^{\circ}$
$\text{C.}$ $48^{\circ}$
$\text{D.}$ $36^{\circ}$
如果一个三位数中任意两个相邻数字之差的绝对值不超过 1 , 则称该三位数为 “平稳数”. 用 $1,2,3$ 这 三个数字随机组成一个无重复数字的三位数, 恰好是“平稳数”的概率为
$\text{A.}$ $\frac{5}{9}$
$\text{B.}$ $\frac{1}{2}$
$\text{C.}$ $\frac{1}{3}$
$\text{D.}$ $\frac{2}{9}$
如图, 点 $E$ 在正方形 $A B C D$ 的对角线 $A C$ 上, $E F \perp A B$ 于点 $F$, 连接 $D E$ 并延长, 交边 $B C$ 于点 $M$, 交边 $A B$ 的延长线于点 $G$. 若 $A F=2, F B=1$, 则 $M G=(\quad)$
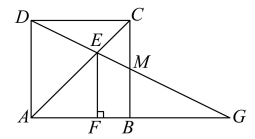
$\text{A.}$ $2 \sqrt{3}$
$\text{B.}$ $\frac{3 \sqrt{5}}{2}$
$\text{C.}$ $\sqrt{5}+1$
$\text{D.}$ $\sqrt{10}$
如图, $E$ 是线段 $A B$ 上一点, $\triangle A D E$ 和 $\triangle B C E$ 是位于直线 $A B$ 同侧的两个等边三角形, 点 $P, F$ 分别是 $C D, A B$ 的中点. 若 $A B=4$, 则下列结论错误的是
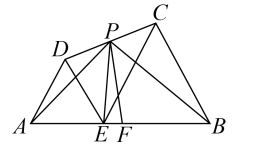
$\text{A.}$ $P A+P B$ 的最小值为 $3 \sqrt{3}$
$\text{B.}$ $P E+P F$ 的最小值为 $2 \sqrt{3}$
$\text{C.}$ $\triangle C D E$ 周长的最小值为 6
$\text{D.}$ 四边形 $A B C D$ 面积的最小值为 $3 \sqrt{3}$
填空题 （共 4 题 ），请把答案直接填写在答题纸上
据统计, 2023 年第一季度安徽省采矿业实现利润总额 74.5 亿元, 其中 74.5 亿用科学记数法表示 为
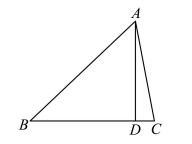
清初数学家梅文鼎在著作《平三角举要》中, 对南宋数学家秦九韶提出的计算三角形面积的“三斜求积 术” 给出了一个完整的证明, 证明过程中创造性地设计直角三角形, 得出了一个结论: 如图, $A D$ 是锐角 $\triangle A B C$ 的高, 则 $B D=\frac{1}{2}\left(B C+\frac{A B^2-A C^2}{B C}\right)$. 当 $A B=7, B C=6, A C=5$ 时, $C D=$
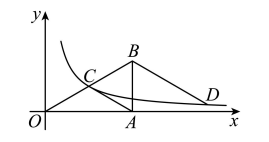
如图, $O$ 是坐标原点, Rt $\triangle O A B$ 的直角顶点 $A$ 在 $x$ 轴的正半轴上, $A B=2, \angle A O B=30^{\circ}$, 反比例函 数 $y=\frac{k}{x}(k>0)$ 的图象经过斜边 $O B$ 的中点 $C$.
(1) $k=$ ________
(2) $D$ 为该反比例函数图象上的一点, 若 $D B \| A C$, 则 $O B^2-B D^2$ 的值为 ________
解答题 （共 9 题 ），解答过程应写出必要的文字说明、证明过程或演算步骤
先化简, 再求值: $\frac{x^2+2 x+1}{x+1}$, 其中 $x=\sqrt{2}-1$.
根据经营情况, 公司对某商品在甲、乙两地的销售单价进行了如下调整: 甲地上涨 $10 \%$, 乙地降价 5 元, 已知销售单价调整前甲地比乙地少 10 元, 调整后甲地比乙地少 1 元, 求调整前甲、乙两地该商品的销 售单价.
如图, 在由边长为 1 个单位长度的小正方形组成的网格中, 点 $A, B, C, D$ 均为格点 (网格线的交点).
(1) 画出线段 $A B$ 关于直线 $C D$ 对称的线段 $A_1 B_1$;
(2) 将线段 $A B$ 向左平移 2 个单位长度, 再向上平移 1 个单位长度, 得到线段 $A_2 B_2$, 画出线段 $A_2 B_2$;
(3) 描出线段 $A B$ 上的点 $M$ 及直线 $C D$ 上的点 $N$, 使得直线 $M N$ 垂直平分 $A B$.
【观察思考】
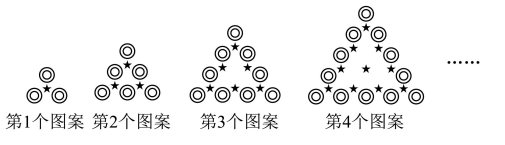
【规律发现】 请用含 $n$ 的式子填空:
(1) 第 $n$ 个图案中“○”的个数为
(2)
第1个图案中★ 的个数可表示为 $ \frac{1 \times 2}{2}$
第2个图案中★ 的个数可表示为 $ \frac{2 \times 3}{2}$
第3个图案中★ 的个数可表示为 $ \frac{3 \times 4}{2}$
第4个图案中★ 的个数可表示为 $ \frac{4 \times 5}{2}$
第n个图案中★ 的个数可表示为
(3) 结合图案中★的排列方式及上述规律, 求正整数 $n$, 使得连续的正整数之和 $1+2+3+\cdots+n$ 等于 第 $n$ 个图案中○ 的个数的 2 倍.
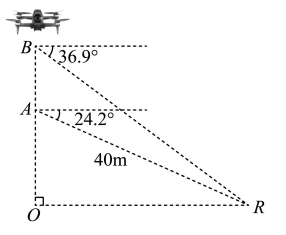
如图, $O, R$ 是同一水平线上的两点, 无人机从 $O$ 点坚直上升到 $A$ 点时, 测得 $A$ 到 $R$ 点的距离为 $40 m, R$ 点的俯角为 $24.2^{\circ}$, 无人机继续坚直上升到 $B$ 点, 测得 $R$ 点的俯角为 $36.9^{\circ}$. 求无人机从 $A$ 点到 $B$ 点的上升 高度 $A B$ (精确到 $0.1 \mathrm{~m}$ ). 参考数据: $\sin 24.2^{\circ} \approx 0.41, \cos 24.2^{\circ} \approx 0.91, \tan 24.2^{\circ} \approx 0.45, \sin 36.9^{\circ} \approx$ $0.60, \cos 36.9^{\circ} \approx 0.80, \tan 36.9^{\circ} \approx 0.75$.
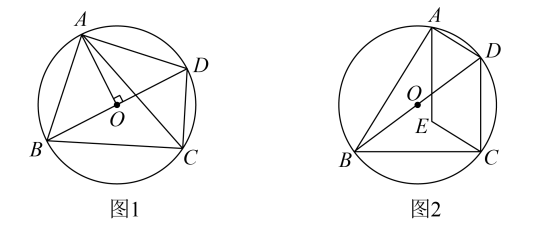
已知四边形 $A B C D$ 内接于 $\odot O$, 对角线 $B D$ 是 $\odot O$ 的直径.
(1) 如图 1, 连接 $O A, C A$, 若 $O A \perp B D$, 求证; $C A$ 平分 $\angle B C D$;
(2) 如图 2, $E$ 为 $\odot O$ 内一点, 满足 $A E \perp B C, C E \perp A B$, 若 $B D=3 \sqrt{3}, A E=3$, 求弦 $B C$ 的长.
端午节是中国的传统节日, 民间有端午节吃粽子的习俗, 在端午节来临之际, 某校七、八年级开展了 一次“包粽子”实践活动, 对学生的活动情况按 10 分制进行评分, 成绩（单位: 分) 均为不低于 6 的整数、 为了解这次活动的效果, 现从这两个年级各随机抽取 10 名学生的活动成绩作为样本进行活整理, 并绘制统 计图表, 部分信息如下:
七年级10名学生活动成绩扇形统计图
八年级 10名学生活动成绩统计表
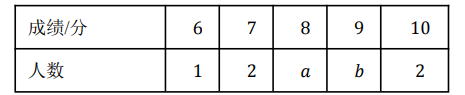
已知八年级 10 名学生活动成绩的中位数为 8.5 分.
请根据以上信息, 完成下列问题:
(1) 样本中, 七年级活动成绩为 7 分的学生数是 , 七年级活动成绩的众数为 分;
(2) $a=$ , $b=$
(3) 若认定活动成绩不低于 9 分为“优秀”, 根据样本数据, 判断本次活动中优秀率高的年级是否平均成绩 也高, 并说明理由.
在 Rt $\triangle A B C$ 中, $M$ 是斜边 $A B$ 的中点, 将线段 $M A$ 绕点 $M$ 旋转至 $M D$ 位置, 点 $D$ 在直线 $A B$ 外, 连接 $A D, B D$.
(1) 如图 1, 求 $\angle A D B$ 的大小;
(2) 已知点 $D$ 和边 $A C$ 上的点 $E$ 满足 $M E \perp A D, D E \| A B$.
( i ) 如图 2, 连接 $C D$, 求证: $B D=C D$;
(ii) 如图 3, 连接 $B E$, 若 $A C=8, B C=6$, 求 $\tan \angle A B E$ 的值.
在平面直角坐标系中, 点 $O$ 是坐标原点, 抛物线 $y=a x^2+b x(a \neq 0)$ 经过点 $A(3,3)$, 对称轴为直线 $x=2$.
(1) 求 $a, b$ 的值;
(2) 已知点 $B, C$ 在抛物线上, 点 $B$ 的横坐标为 $t$, 点 $C$ 的横坐标为 $t+1$. 过点 $B$ 作 $x$ 轴的垂线交直线 $O A$ 于点 $D$, 过点 $C$ 作 $x$ 轴的垂线交直线 $O A$ 于点 $E$.
(i) 当 $0 < t < 2$ 时, 求 $\triangle O B D$ 与 $\triangle A C E$ 的面积之和;
(ii) 在抛物线对称轴右侧, 是否存在点 $B$, 使得以 $B, C, D, E$ 为顶点的四边形的面积为 $\frac{3}{2}$ ? 若存在, 请 求出点 $B$ 的横坐标 $t$ 的值; 若不存在, 请说明理由.