单选题 （共 8 题 ），每题只有一个选项正确
设集合 $A=\left\{x \in N^* \mid 2^x < 4\right\}, B=\{x \in N \mid-1 < x < 2\}$, 则 $A \cup B=$
$\text{A.}$ $\{x \mid-1 < x < 2\}$
$\text{B.}$ $\{x \mid x < 2\}$
$\text{C.}$ $\{0,1\}$
$\text{D.}$ $\{1\}$
若复数 $z$ 满足 $|z|=|z+2 \mathrm{i}|$, 其中 $\mathrm{i}$ 是虚数单位, 则复数 $z$ 的虚部是
$\text{A.}$ 1
$\text{B.}$ -1
$\text{C.}$ i
$\text{D.}$ -i
函数 $f(x)=\log _a|x|+1(0 < a < 1)$ 的图象大致为
$\text{A.}$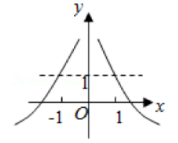 
$\text{B.}$ 
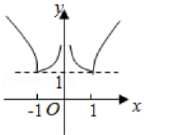$\text{C.}$ 
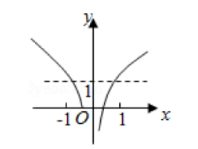$\text{D.}$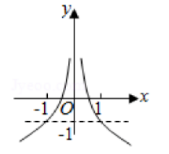 
快递公司计划在某货运枢纽附近投资配建货物分拣中心. 假定每月的土地租金成本与分拣中心到货运 枢纽的距离成反比, 每月的货物运输成本与分拣中心到货运枢纽的距离成正比. 经测算, 如果在距离货 运枢纽 $10 \mathrm{~km}$ 处配建分拣中心, 则每月的土地租金成本和货物运输成本分别为 2 万元和 8 万元. 要使得 两项成本之和最小, 分拣中心和货运枢纽的距离应设置为
$\text{A.}$ $5 \mathrm{~km}$
$\text{B.}$ $6 \mathrm{~km}$
$\text{C.}$ $7 \mathrm{~km}$
$\text{D.}$ $8 \mathrm{~km}$
八卦是中国古老文化的深奥概念, 下图示意太极八卦图. 现将一副八卦简化为正八边形 $A B C D E F G H$, 设其边长为 $a$, 中心为 $O$, 则下列选项中不正确的是
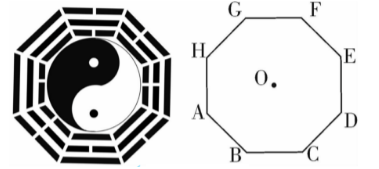
$\text{A.}$ $\overrightarrow{A B} \cdot \overrightarrow{A C}=\overrightarrow{A B} \cdot \overrightarrow{A D}$
$\text{B.}$ $\overrightarrow{E G}$ 和 $\overrightarrow{H D}$ 是一对相反向量
$\text{C.}$ $\overrightarrow{O A} \cdot \overrightarrow{O B}+\overrightarrow{O C} \cdot \overrightarrow{O F}=0 $
$\text{D.}$ $|\overrightarrow{A B}-\overrightarrow{B C}+\overrightarrow{C D}+\overrightarrow{E F}-\overrightarrow{F G}|=a$
已知 $\sin \left(\frac{\pi}{6}-\alpha\right)=\frac{\sqrt{2}}{3}$, 则 $\cos \left(2 \alpha-\frac{4 \pi}{3}\right)$ 等于
$\text{A.}$ $-\frac{5}{9}$
$\text{B.}$ $\frac{5}{9}$
$\text{C.}$ $-\frac{1}{3}$
$\text{D.}$ $\frac{1}{3}$
已知 $\left\{a_n\right\}$ 是公差为 3 的等差数列, 其前 $n$ 项的和为 $S_n$, 设甲: $\left\{a_n\right\}$ 的首项为零; 乙: $S_2+3$ 是 $S_1+3$ 和 $S_3+$ 3 的等比中项, 则
$\text{A.}$ 甲是乙的充分不必要条件
$\text{B.}$ 甲是乙的必要不充分条件
$\text{C.}$ 甲是乙的充要条件
$\text{D.}$ 甲既不是乙的充分条件也不是乙的必要条件
已知函数 $f(x)=x^2+2^x+2^{-x}$, 若不等式 $f(1-a x) < f\left(2+x^2\right)$ 对任意 $x \in R$ 恒成立, 则实数 $a$ 的取值范 围是
$\text{A.}$ $(-2 \sqrt{3}, 2)$
$\text{B.}$ $(-2 \sqrt{3}, 2 \sqrt{3})$
$\text{C.}$ $(-2,2 \sqrt{3})$
$\text{D.}$ $(-2,2)$
多选题 （共 4 题 ），每题有多个选项正确
随着国民经济的快速发展和人民生活水平的不断提高, 我国社会物流需求不断增加, 物流行业前景广 阔. 社会物流总费用与 $G D P$ 的比率是反映地区物流发展水平的指标, 下面是 $2017-2022$ 年我国社会物 流总费用与 $G D P$ 的比率统计, 则
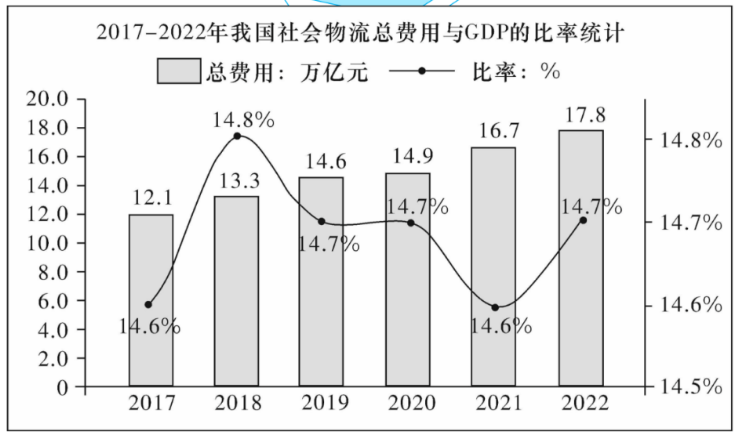
$\text{A.}$ $2018-2022$ 这 5 年我国社会物流总费用逐年增长, 且 2021 年增长的最多
$\text{B.}$ $2017-2022$ 这 6 年我国社会物流总费用的 $70 \%$ 分位数为 14.9 万亿元
$\text{C.}$ $2017-2022$ 这 6 年我国社会物流总费用与 $G D P$ 的比率的极差为 $0.3 \%$
$\text{D.}$ 2022 年我国的 $G D P$ 超过了 121 万亿元
已知 $\left\{a_n\right\}$ 是各项均为正数的等比数列, 其前 $n$ 项和为 $S_n$, 且 $\left\{S_n\right\}$ 是等差数列, 则下列结论正确的是
$\text{A.}$ $\left\{a_n+S_n\right\}$ 是等差数列
$\text{B.}$ $\left\{a_n \cdot S_n\right\}$ 是等比数列
$\text{C.}$ $\left\{a_n^2\right\}$ 是等差数列
$\text{D.}$ $\left\{\frac{S_n}{n}\right\}$ 是等比数列
先将函数 $f(x)=2 \sin x$ 的图象向右平移 $\frac{\pi}{6}$ 个单位长度, 再将横坐标缩短为原来的 $\frac{1}{2}$ (纵坐标不变), 得到 函数 $g(x)$ 的图象, 则下列关于函数 $g(x)$ 的说法中正确的是
$\text{A.}$ 在 $\left(\frac{\pi}{6}, \frac{5 \pi}{12}\right)$ 上单调递增
$\text{B.}$ 当 $x \in\left[\frac{\pi}{2}, \pi\right]$ 时, 函数 $g(x)$ 的值域是 $[-2,1]$
$\text{C.}$ 其图象关于直线 $x=\frac{5 \pi}{6}$ 对称
$\text{D.}$ 直线 $y=2 \sqrt{3} x-1$ 为曲线 $y=g(x)$ 的切线
如图, 在棱长为 3 的正方体 $A B C D-A_1 B_1 C_1 D_1$ 中, 点 $P$ 是平面 $A_1 B C_1$ 内的一个动点, 且满足 $P D+P B_1$ $=2+\sqrt{13}$, 则下列结论正确的是
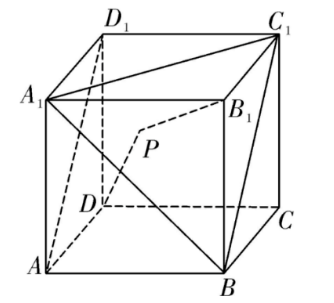
$\text{A.}$ $B_1 D \perp P B$
$\text{B.}$ 点 $P$ 的轨迹是一个半径为 $\sqrt{2}$ 的圆
$\text{C.}$ 直线 $B_1 P$ 与平面 $A_1 B C_1$ 所成角为 $\frac{\pi}{3}$
$\text{D.}$ 三棱雉 $P-B B_1 C_1$ 体积的最大值为 $\frac{3}{2}+\frac{\sqrt{6}}{2}$
填空题 （共 4 题 ），请把答案直接填写在答题纸上
高二年级体锻课时间提供三项体育活动, 足球、篮球、兵乓球供学生选择. 甲、乙两名学生从这三项运动 中随机选一种, 且他们的选择情况相互独立互不影响. 在甲学生选择足球的前提下, 两人的选择不同的 概率为
正实数 $x, y$ 满足 $\frac{1}{x}+\frac{4}{y}=2$, 且不等式 $x+\frac{y}{4} \geqslant m^2-m$ 恒成立, 则实数 $m$ 的取值范围为
已知三棱雉 $A-B C D$ 中, $B C=C D=2, B D=2 \sqrt{2}, A C=2 \sqrt{2}, \triangle A B D$ 是等边三角形, 则三棱雉 $A-$ $B C D$ 的外接球的表面积为
在直角 $\triangle A B C$ 中, $A B \perp A C, A C=\sqrt{3}, A B=1$, 平面 $A B C$ 内动点 $P$ 满足 $C P=1$, 则 $\overrightarrow{A P} \cdot \overrightarrow{B P}$ 的最小值 为
解答题 （共 6 题 ），解答过程应写出必要的文字说明、证明过程或演算步骤
已知 $\triangle A B C$ 中角 $A, B, C$ 所对的边分别为 $a, b, c$, 且满足 $2 c \sin A \cos B+2 b \sin A \cos C=\sqrt{3} a, c>a$.
(1) 求角 $A$;
(2) 若 $b=2, \triangle A B C$ 的面积 $2 \sqrt{3}, D$ 是 $B C$ 边上的点, 且 $\overrightarrow{C D}=3 \overrightarrow{D B}$, 求 $A D$.
已知数列 $\left\{x_n\right\}$ 的首项为 1 , 且 $x_1+\dfrac{x_2}{2}+\cdots+\dfrac{x_{n-1}}{2^{n-2}}+\dfrac{x_n}{2^{n-1}}=\dfrac{n x_{n+1}}{2^n}$.
(1) 求数列 $\left\{x_n\right\}$ 的通项公式;
(2) 若 $b_n=\frac{1}{2}(2 n+1)\left(x_{n+1}-x_n\right), S_n$ 为 $\left\{b_n\right\}$ 前 $n$ 项的和, 求 $S_n$.
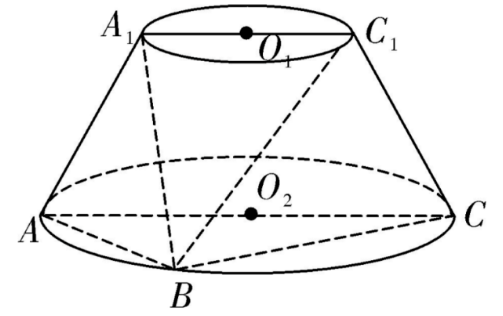
如图, 圆台 $O_1 O_2$ 的轴截面为等腰梯形 $A_1 A C C_1, A C=2 A A_1=2 A_1 C_1=4, B$ 为下底面圆周上异于 $A, C$ 的 点.
(1) 在平面 $B C C_1$ 内, 过 $C_1$ 作一条直线与平面 $A_1 A B$ 平行, 并说明理由;
(2) 若四棱雉 $B-A_1 A C C_1$ 的体积为 $2 \sqrt{3}$, 求平面 $A_1 A B$ 与平面 $C_1 C B$ 夹角的余弦值.
甲、乙两名运动员进行乒乓球比赛, 规定每局比赛胜者得 1 分, 负者得 0 分, 平局双方均得 0 分, 比赛一直 进行到一方比另一方多两分为止, 多得两分的一方赢得比赛. 已知每局比赛中, 甲获胜的概率为 $\alpha$, 乙获 胜的概率为 $\beta$, 两人平局的概率为 $\gamma(\alpha+\beta+\gamma=1, \alpha>0, \beta>0, \gamma \geqslant 0)$, 且每局比赛结果相互独立.
(1) 若 $\alpha=\frac{1}{2}, \beta=\frac{1}{3}, \gamma=\frac{1}{6}$, 求甲学员恰好在第 4 局比赛后赢得比赛的概率;
(2) 当 $\gamma=0$ 时, 若比赛最多进行 5 局, 求比赛结束时比赛局数 $X$ 的分布列及期望 $E(X)$ 的最大值.
已知正项数列 $\left\{a_n\right\}$ 满足: $a_1=3$, 且 $a_n\left(a_{n+1}^2-1\right)=2\left(a_n^2-1\right) a_{n+1}, n \in N^*$.
(1) 设 $b_n=a_n-\frac{1}{a_n}$, 求数列 $\left\{b_n\right\}$ 的通项公式;
(2) 设 $c_n=a_n^2+\frac{1}{a_n^2}$, 求数列 $\left\{c_n\right\}$ 的前 $n$ 项和 $T_n$, 并确定最小正整数 $n$, 使得 $T_n$ 为整数.
设双曲线 $C: \frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0, b>0)$ 的右焦点为 $F$, 点 $O$ 为坐标原点, 过点 $F$ 的直线 $l$ 与 $C$ 的右支相交 于 $A, B$ 两点.
(1) 当直线 $l$ 与 $x$ 轴垂直时, $O A \perp O B$, 求 $C$ 的离心率;
(2) 当 $C$ 的焦距为 2 时, $\angle A O B$ 恒为锐角, 求 $C$ 的实轴长的取值范围.