单选题 （共 8 题 ），每题只有一个选项正确
若集合 $A=\left\{x \mid \frac{x+3}{x-3} \leq 0\right\}, B=\{-3,-1,0,3,4\}$, 则 $A \cap B$ 的元素个数为
$\text{A.}$ 2
$\text{B.}$ 3
$\text{C.}$ 4
$\text{D.}$ 5
设 $z=a+b i(a, b \in \boldsymbol{R})$ 在复平面内对应的点为 $M$, 则“点 $M$ 在第四象限”是“ $a b < 0$ ”的
$\text{A.}$ 充分不必要条件
$\text{B.}$ 必要不充分条件
$\text{C.}$ 既不充分也不必要条件
$\text{D.}$ 充要条件
已知 $\left\{a_n\right\}$ 是各项不相等的等差数列, 若 $a_1=4$, 且 $a_2, a_4, a_8$ 成等比数列, 则数列 $\left\{a_n\right\}$ 的前 6 项和 ( ).
$\text{A.}$ 84
$\text{B.}$ 144
$\text{C.}$ 288
$\text{D.}$ 110
$\mid$ 已知向量 $\vec{a}, \vec{b}$ 满足 $|\vec{a}|=2, \vec{b}=(1,1),|\vec{a}+\vec{b}|=\sqrt{10}$, 则向量 $\vec{a}$ 在向量 $\vec{b}$ 上的投影向量的坐标为
$\text{A.}$ $\left(\frac{\sqrt{2}}{2}, \frac{\sqrt{2}}{2}\right)$
$\text{B.}$ $(1,1)$
$\text{C.}$ $(-1,-1)$
$\text{D.}$ $\left(-\frac{\sqrt{2}}{2}, \frac{\sqrt{2}}{2}\right)$
函数 $f(x)=\left(\frac{1-e^x}{1+e^x}\right) \cos \left(\frac{\pi}{2}-x\right)$ 的部分图象大致形状是
$\text{A.}$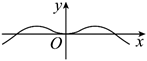 
$\text{B.}$ 
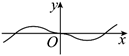$\text{C.}$ 
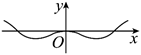$\text{D.}$ 
立德学校于三月份开展学雷锋主题活动, 某班级 5 名女生和 2 名男生, 分成两个小组去两地参加志愿者活 动, 每小组均要求既要有女生又要有男生, 则不同的分配方案有 ________ 种
$\text{A.}$ 20
$\text{B.}$ 4
$\text{C.}$ 60
$\text{D.}$ 80
刍(chú)甍(méng)是中国古代算数中的一种几何体，其结构特征是：底面为长方形，上棱和底面平行，且长度不等于底面平行的棱长的五面体，是一个对称的楔形体
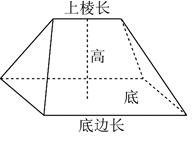
已知一个刍甍底边长为6，底边宽为4，上棱长为2，高为2，则它的表面积是
$\text{A.}$ $24 \sqrt{2}$
$\text{B.}$ $24+24 \sqrt{2}$
$\text{C.}$ $24+24 \sqrt{5}$
$\text{D.}$ $24+16 \sqrt{2}+8 \sqrt{5}$
如图, 粗圆 $C: \frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$ 的左焦点为 $F_1$, 右顶点为 $A$, 点 $Q$ 在 $y$ 轴上, 点 $P$ 在椭圆上, 且满 足 $P Q \perp y$ 轴, 四边形 $F_1 A P Q$ 是等腰梯形, 直线 $F_1 P$ 与 $y$ 轴交于点 $N\left(0, \frac{\sqrt{3}}{4} b\right)$, 则椭圆的离心率为
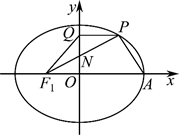
$\text{A.}$ $\frac{1}{4}$
$\text{B.}$ $\frac{\sqrt{3}}{2}$
$\text{C.}$ $\frac{\sqrt{2}}{2}$
$\text{D.}$ $\frac{1}{2}$
多选题 （共 4 题 ），每题有多个选项正确
如图为国家统计局于2022年12月27日发布的有关数据，则
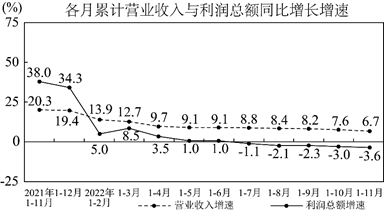
$\text{A.}$ 营业收入增速的中位数为$9.1 \%$
$\text{B.}$ 营业收入增速极差为 $13.6 % $
$\text{C.}$ 利润总额增速越来越小
$\text{D.}$ 利润总额增速的平均数大于$6%$
甲袋中装有 4 个白球, 2 个红球和 2 个黑球, 乙袋中装有 3 个白球, 3 个红球和 2 个黑球. 先从甲袋中随机 取出一球放入乙袋, 再从乙袋中随机取出一球. 用 $A_1, A_2, A_3$ 分别表示田袋取出的球是白球、红球和黑球, 用 $B$ 表示乙袋取出的球是白球，则
$\text{A.}$ $A_1, A_2, A_3$ 两两互斥
$\text{B.}$ $P\left(B \mid A_2\right)=\frac{1}{3}$
$\text{C.}$ $A_3$ 与 $B$ 是相互独立事件
$\text{D.}$ $P(B)=\frac{1}{3}$
已知 $F_1, F_2$ 是双曲线 $C: \frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0, b>0)$ 的左、右焦点, $A\left(\frac{\sqrt{15}}{2}, \frac{1}{2}\right)$ 是 $C$ 上一点, 若 $C$ 的离心率为 $\frac{2 \sqrt{3}}{3}$, 连结 $A F_2$ 交 $C$ 于点 $B$, 则
$\text{A.}$ $C$ 的方程为 $\frac{x^2}{3}-y^2=1$
$\text{B.}$ $\angle F_1 A F_2=90^{\circ}$
$\text{C.}$ $\triangle F_1 A F_2$ 的周长为 $2 \sqrt{5}+2$
$\text{D.}$ $\triangle A B F_1$ 的内切圆半径为 $\sqrt{5}-\sqrt{3}$
已知函数 $f(x)$ 及其导函数 $f^{\prime}(x)$ 的定义域均为 $\mathrm{R}$, 若 $f\left(x+\frac{2}{3}\right)$ 为奇函数, $f\left(2 x-\frac{1}{3}\right)$ 的图象关于 $y$ 轴对称, 则 下列结论中一定正确的是
$\text{A.}$ $f\left(\frac{2}{3}\right)=0$
$\text{B.}$ $f(0)=f\left(-\frac{2}{3}\right)$
$\text{C.}$ $f^{\prime}(0)=f^{\prime}\left(-\frac{2}{3}\right)$
$\text{D.}$ $f^{\prime}\left(-\frac{1}{3}\right)=0$
填空题 （共 4 题 ），请把答案直接填写在答题纸上
若 $(1-x)^8=a_0+a_1(1+x)+a_2(1+x)^2+\cdots+a_8(1+x)^8$, 则 $a_5=$
若斜率为 $\sqrt{3}$ 的直线与 $y$ 轴交于点 $A$, 与圆 $x^2+y^2=1$ 相切于点 $B$, 则 $|A B|=$
某市统计高中生身体素质的状况, 规定身体素质指标值不小于 60 就认为身体素质合格. 现从全市随机抽取 100 名高中生的身体素质指标值 $x_i(i=1,2,3, \cdots, 100)$, 经计算 $\sum_{i=1}^{100} x_i=7200, \sum_{i=1}^{1 < 0} x_i^{ < }=100 \times\left(72^2+\right.$ 36). 若该市高中生的身体素质指标值服从正态分布 $N\left(\mu, \sigma^2\right)$, 则估计该市高中生身体素质的合格率为 ________
(用百分数作答，精确到 $0.1 \%)$ 参考数据: 若随机变量 $X$ 服从正态分布 $N\left(\mu, \sigma^2\right)$, 则 $P(\mu-\sigma \leq X \leq \mu+\sigma) \approx 0.6827, P(\mu-2 \sigma \leq X \leq \mu+$ $2 \sigma) \approx 0.9545, \quad P(\mu-3 \sigma \leq X \leq \mu+3 \sigma) \approx 0.9973$.
已知函数 $f(x)=\left\{\begin{array}{c}e^{-2 x}-1, x \leq 0 \\ \frac{1}{2} \ln (x+1), x>0\end{array}\right.$. 若 $x(f(x)-a|x|) \leq 0$, 则 $a$ 的取值范围是
解答题 （共 6 题 ），解答过程应写出必要的文字说明、证明过程或演算步骤
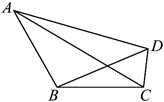
如图, 在四边形 $A B C D$ 中, 已知 $\angle A B C=\frac{2 \pi}{3}, \angle B D C=\frac{\pi}{3}, A B=B C=7 \sqrt{3}$.
(1) 若 $B D=5 \sqrt{3}$, 求 $A D$ 的长;
(2) 求 $\triangle A B D$ 面积的最大值.
记 $S_n$ 为数列 $\left\{a_n\right\}$ 的前 $n$ 项和, 已知 $a_1=1, a_2=\frac{2}{3}$, 且数列 $\left\{4 n S_n+(2 n+3) a_n\right\}$ 是等差数列.
(1) 证明: $\left\{\frac{a_n}{n}\right\}$ 是等比数列, 并求 $\left\{a_n\right\}$ 的通项公式;
(2) 设 $b_n=\left\{\begin{array}{c}3^{n-1} \cdot a_n, n \text { 为奇数 } \\ \frac{n}{a_n}, n \text { 为偶数 }\end{array}\right.$, 求数列 $\left\{b_n\right\}$ 的前 $2 n$ 项和 $T_{2 n}$.
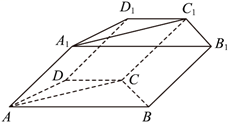
如图, 已知斜四棱柱 $A B C D-A_1 B_1 C_1 D_1$, 底面 $A B C D$ 为等腰梯形, $A B \| C D$, 点 $A_1$ 在底面 $A B C D$ 的射影为 $O$, 且 $A D=B C=C D=A A_1=1, A B=2, A_1 O=\frac{1}{2}, A A_1 \perp B C$.
(1) 求证: 平面 $A B C D \perp$ 平面 $A C C_1 A_1$;
(2) 若 $M$ 为线段 $B_1 D_1$ 上一点, 且平面 $M B C$ 与平面 $A B C D$ 夹角的余弦值为 $\frac{\sqrt{21}}{7}$, 求直线 $A_1 M$ 与平面 $M B C$ 所成角 的正弦值.
第22届亚运会将于2023年9月23日至10月8日在我国杭州举行, 这是我国继北京后第二次举办亚运会. 为迎 接这场体育盛会, 浙江某市决定举办一次亚运会知识竞赛, 该市 $A$ 社区举办了一场选拔赛, 选拔赛分为初赛 和决赛, 初赛通过后才能参加决赛, 决赛通过后将代表 $A$ 社区参加市亚运知识竞赛. 已知 $A$ 社区甲、乙、丙 3 位选手都参加了初赛且通过初赛的概率依次为 $\frac{1}{2} 、 \frac{1}{2} 、 \frac{1}{3}$, 通过初赛后再通过决赛的概率均为 $\frac{1}{3}$, 假设他们之 间通过与否互不影响.
(1) 求这 3 人中至多有 2 人通过初赛的概率;
(2) 求这 3 人中至少有 1 人参加市知识竞赛的概率;
(3)某品牌商赞助了 $A$ 社区的这次知识竞赛, 给参加选拔赛的选手提供了两种奖励方案:
方案一: 参加了选拔赛的选手都可参与抽奖, 每人抽奖 1 次, 每次中奖的概率均为 $\frac{1}{2}$, 且每次抽奖互不影响, 中奖一次奖励 600 元;
方案二: 只参加了初赛的选手奖励 200 元, 参加了决赛的选手奖励 500 元.
若品牌商希望给予选手更多的奖励, 试从三人奖金总额的数学期望的角度分析, 品牌商选择哪种方案更好.
已知抛物线 $C: x^2=2 p y(p>0)$ 的焦点为 $F$, 准线 $l$ 与抛物线 $C$ 的对称轴的交点为 $K$, 点 $D(2, t)$ 在抛物线 $C$ 上, 且 $|D K|=\sqrt{2}|D F|$.
(1) 求抛物线 $C$ 的方程;
(2) 若直线 $l_1: k x-y-2 k=0(k>0)$ 交抛物线 $C$ 于 $A\left(x_1, y_1\right), B\left(x_2, y_2\right)\left(x_1>x_2\right)$ 两点, 点 $A$ 在 $y$ 轴上的投影为 $E$, 直线 $A E$ 分别与直线 $O B$ ( $O$ 为坐标原点) 交于点 $Q$, 与直线 $l_2: y=x$ 交于点 $P$, 记 $\triangle O A P$ 的面积为 $S_1, \triangle O P Q$ 的面积为 $S_2$, 求证: $S_1=S_2$.
已知函数 $f(x)=a x-\ln x-\frac{a}{x}$.
(1) 若 $x>1, f(x)>0$, 求实数 $a$ 的取值范围;
(2) 设 $x_1, x_2$ 是函数 $f(x)$ 的两个极值点, 证明: $\left|f\left(x_1\right)-f\left(x_2\right)\right| < \frac{\sqrt{1-4 a^2}}{a}$.