单选题 (共 10 题 ),每题只有一个选项正确
与 $\sqrt{2}$ 是同类二次根式的是
$\text{A.}$ $\sqrt{4}$
$\text{B.}$ $\sqrt{6}$
$\text{C.}$ $\sqrt{8}$
$\text{D.}$ $\sqrt{12}$
若 $\frac{a}{b}=\frac{2}{3}$, 则 $\frac{a+b}{b}$ 等于
$\text{A.}$ $\frac{1}{3}$
$\text{B.}$ $\frac{2}{3}$
$\text{C.}$ $\frac{3}{5}$
$\text{D.}$ $\frac{5}{3}$
在 Rt $\triangle A B C$ 中, $\angle C=90^{\circ}, \sin A=\frac{3}{5}$, 则 $\cos A$ 的值是
$\text{A.}$ $\frac{3}{5}$
$\text{B.}$ $\frac{3}{4}$
$\text{C.}$ $\frac{4}{5}$
$\text{D.}$ $\frac{5 \sqrt{34}}{34}$
一元二次方程 $x(x-3)=x$ 的解是
$\text{A.}$ $x=0$
$\text{B.}$ $x=3$
$\text{C.}$ $x_1=0, x_2=3$
$\text{D.}$ $x_1=0, x_2=4$
一个不透明的盒子中装有 1 个红球和 2 个白球, 它们除颜色不同外其它都相同. 若从中随机摸出一个球, 则下列叙述正确的是
$\text{A.}$ 摸到黑球是不可能事件
$\text{B.}$ 摸到白球是必然事件
$\text{C.}$ 摸到红球与摸到白球的可能性相等
$\text{D.}$ 摸到红球比摸到白球的可能性大
用配方法解方程 $x^2-6 x-1=0$, 若配方后结果为 $(x-m)^2=10$, 则 $m$ 的值为
$\text{A.}$ $\pm 3$
$\text{B.}$ $3$
$\text{C.}$ $-3$
$\text{D.}$ $6$
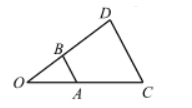
如图, 以点 $O$ 为位似中心, 将 $\triangle O A B$ 放大后得到 $\triangle O C D, O A=3, A C=4$, 则 $\frac{A B}{C D}$ 等于
$\text{A.}$ $\frac{3}{7}$
$\text{B.}$ $\frac{4}{7}$
$\text{C.}$ $\frac{3}{4}$
$\text{D.}$ $\frac{3}{5}$
如图, 在 $\odot O$ 中, $\angle A O B=120^{\circ}$, 点 $P 、 Q$ 分别是 $\overparen{A P B}$ 与 $\overparen{A B}$ 上的动点, 则 $\angle A P Q$ 的度数不可能是

$\text{A.}$ $50^{\circ}$
$\text{B.}$ $55^{\circ}$
$\text{C.}$ $60^{\circ}$
$\text{D.}$ $65^{\circ}$
已知 “ $\alpha$ 为锐角时, $\sin \alpha$ 随着 $\alpha$ 的增大而增大”, 则 $\sin 37^{\circ}$ 的值更靠近
$\text{A.}$ $\frac{2}{5}$
$\text{B.}$ $\frac{3}{5}$
$\text{C.}$ $\frac{4}{5}$
$\text{D.}$ $\frac{5}{6}$
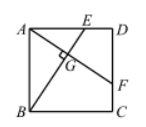
如图, 在正方形 $A B C D$ 中, 点 $E 、 F$ 分别在边 $A D$ 和 $C D$ 上, $ A F \perp B E$, 垂足为 $G$, 若 $\frac{A E}{E D}=2$, 则 $\frac{A G}{G F}$ 的值为
$\text{A.}$ $\frac{4}{5}$
$\text{B.}$ $\frac{5}{6}$
$\text{C.}$ $\frac{6}{7}$
$\text{D.}$ $\frac{7}{8}$
填空题 (共 6 题 ),请把答案直接填写在答题纸上
若二次根式 $\sqrt{x-1}$ 有意义, 则 $x$ 可以是 (写出一个 $x$ 的 值即可).
二次函数 $y=2 x^2-3 x+1$ 的图象与 $y$ 轴的交点坐标为
如图, 某商场自动扶梯 $A B$ 的坡度 $i=1: 2.5$, 过点 $B$ 作 $B C \perp A D$, 垂足为 $C$. 若 $A C$ 的长为 10 米, 则高度 $B C$ 为 ________ 米.
已知 $m$ 是方程 $x^2-2 x-1=0$ 的一个根, 则 $3-m^2+2 m=$,
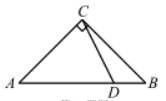
如图, 在 $\triangle A B C$ 中, $\angle A C B=90^{\circ}, A C=B C, D$ 是边 $A B$ 上的 一点, 若 $A D=\frac{3}{4} A B$, 则 $\tan \angle D C B=$
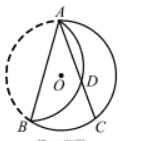
如图, $A B 、 A C$ 是 $\odot O$ 的弦(不是直径), 将 $\overparen{A B}$ 洁 $A B$ 翻折交 $A C$ 于点 $D$, 若 $\overparen{A B}=\overparen{A C}, \overparen{A D}=\overparen{B D}$, 则 $\frac{A D}{C D}=$
解答题 (共 9 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
计算: $\sqrt{2}(\sqrt{3}-\sqrt{2})+\frac{\sqrt{12}-\sqrt{3}}{\sqrt{3}}$.
小明在解方程 $x^2-5 x=-3$ 的过程中出现了错误, 其解答如下:
解: $\because a=1, b=-5, c=-3$, ...........第一步
$\therefore b^2-4 a c=(-5)^2-4 \times 1 \times(-3)=37$ ...第一步
$\therefore x=\frac{5 \pm \sqrt{37}}{2}$ ...第三步
$\therefore x_1=\frac{5+\sqrt{37}}{2}, x_2=\frac{5-\sqrt{37}}{2}$. $\cdots$ ...第四步
(1)问:小明的解答是从第 步开始出错的;
(2)请写出本題正确的解答.
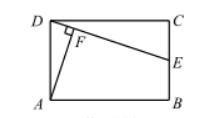
如图, 在矩形 $A B C D$ 中, 点 $E$ 在边 $B C$ 上, $A F \perp D E$, 垂足为 $F, A D=4, C E=2$, $D E=2 \sqrt{10}$, 求 $D F$ 的长.
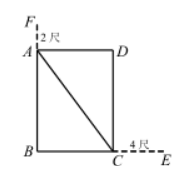
我国古代数学家梅埶成在其著作 《增删算法统宗》中, 有诗如下: 今有门厅一座, 不知门 广高低. 长竿横进使归室, 争奈门狭四尺. 随即坚竿过去, 亦长二尺无疑. 两陗斜去恰方齐, 请 问三色各几? 意思是: 今有一房门, 不知宽与高, 长竿横起进门入室, 门的宽度比长竿小 4 尺; 将长笨直立过门, 门的高度比长竿小 2 尺. 将长竿斜放穿过门的对角, 恰好进门. 试问门的宽、 高和长䇢各是多少尺?
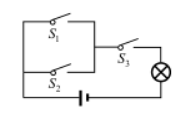
小明学习物理 《电流和电路》后设计如图所示的一个电路图, 其中 $S_1 、 S_2 、 S_3$ 分别表示三 个可开闭的开关, “ $\otimes$ 表示小灯泡, “‖”表示电池.
(1) 当开关 $S_1$ 闭合时, 再随机闭合开关 $S_2$ 或 $S_1$ 其中一个, 直接写出小奵泡发光的概率;
(2)当随机闭合开关 $S_1 、 S_2 、 S_3$ 中的两个, 试用树状图或列表法求小灯泡发光的概率,
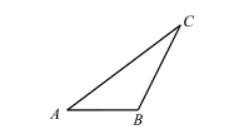
如图, 在 $\triangle A B C$ 中, $\angle A B C$ 是钝角.
(1) 求作 $\odot O$, 使得圆心 $O$ 在边 $A C$ 上, 且 $\odot O$ 经过点 $B 、 C$ (要求: 尺规作图, 不写作法, 保留作图癏迹);
(2) 在(1)的条件下, 设 $A C$ 与 $\odot O$ 的另一个交点为 $D$, 且 $A C=2 A B=4 A D$.
求证: $A B$ 是 $\odot O$ 的切线.
某公司研发了一款产品投放市场, 已知每件产品的成本为 80 元, 试销售一段时间后统计每 天的销售量 $y$ (件)与㫿价 $x$ (元/件)之间的部分数据如下表:

(1)根据表中数据, 求出 $y$ 与 $x$ 之间满足的函数关系式;
(2)物价部门规定单件利泀率不超过 $15 \%$,在(1)的条件下, 当产品售价不低于成本时, 售价 定为多少元, 公司每天获得的利润最大? 求出最大值.
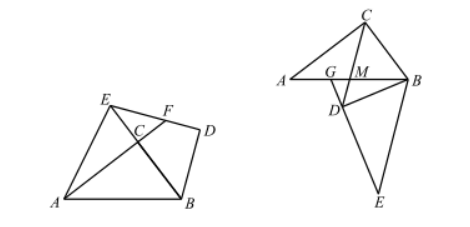
在 Rt $\triangle A B C$ 中, $\angle A C B=90^{\circ}$, 将 Rt $\triangle A B C$ 绕点 $B$ 旋转一定的角度得到 Rt $\triangle E B D$.
(1) 如图 1, 当边 $B E$ 恰好经过点 $C$ 时, 边 $A C$ 的延长线交 $E D$ 于点 $F$, 连接 $A E$.
求证: $\angle A F E=2 \angle E A F$;
(2)如图 2, 当点 $D$ 恰好在 $\triangle A B C$ 中线 $C M$ 的延长线上, 且 $C M=2 M D$ 时, $E D$ 的延长线交 $A B$ 于点 $G$, 求 $\frac{A G}{B C}$ 的值.
在平面直角坐标系 $x O y$ 中, 已知抛物线 $y=a x^2+b x-\sqrt{3}(a \neq 0)$ 经过 $A(-1,0) 、 B(3,0)$ 两点, 交 $y$ 轴于点 $C$, 顶点为 $E$. 过线段 $O B$ 上动点 $F$ 作 $C F$ 的垂线交 $B C$ 于点 $D$, 直线 $D E$ 交 $y$ 轴于点 $G$.
(1)求抛物线的解析式;
(2)若 $C G=C D$, 求线段 $O F$ 的长;
(3)连接 $C E$, 求 $\triangle C D E$ 面积的最小值.