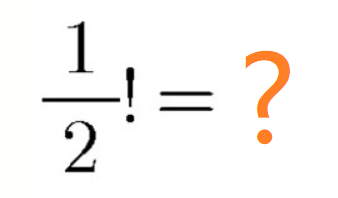填空题 (共 10 题 ),请把答案直接填写在答题纸上
已知 $\left(m^2+\frac{1}{m^2}-4\right)^2=36$,求 $m-\frac{1}{m}$ 的值
化简: $ \cos x \cos 2 x \cos 4 x \cdots \cos 2^n x $
若 $a>0, b>0$, 且 $a+b=2$, 则 $\frac{1}{a}+\frac{1}{b}$ 的最小值为
已知 $x>0, y>0$, 且 $x+2 y=1$, 则 $\frac{2 y}{x+1}+\frac{1}{2 y}$ 的最小值为
若正数 $x, y$ 满足 $x^2+4 y^2+x+2 y=1$, 则 $x y$ 的最大值为
已知正实数 $x, y$ 满足 $x y+2 x+3 y=42$, 则 $x y+5 x+4 y$ 的最小值为
若 $a>2 b>0$, 则 $(a-b)^2+\frac{9}{b(a-2 b)}$ 的最小值为
已知实数 $a, b, c$ 满足 $a^2+b^2+c^2=1$, 则 $a b+b c+2 c a$ 的最大值为
非负实数 $x$, $y$ 满足 $x^2+4 y^2+4 x y+4 x^2 y^2=32$, 则 $\sqrt{7}(x+2 y)+2 x y$ 的最大 值为
已知 $x, y \geq 0, x+y \leq 1$, 求 $4 x^2+4 y^2+(1-x-y)^2$ 的最小值
解答题 (共 4 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
说到方程,最简单的是一元一次方程,就是一个未知数,一个方程构成的,还有二元一次方程组,三元一次方程组,他们的未知数个数与方程个数是相等的,但还有一类方程,未知数个数多于方程的个数,比如:,是由两个未知数,一个方程构成的,这类方程的解由无数多个,由于这类方程的解是不定的,数学上就把它叫做不定方程.
对不定方程的研究,我国古代很早就开始了,《九章算术》方程章中的第“5家共井问题”,就是突出的一例,题目大意是:
五户人家各出固定长度的绳索作井绳,已知甲户 2 绳加乙户 1绳、乙户 3 绳加丙户 1 绳、丙户 4 绳加丁户 1 绳、丁户 5 绳加戊户 1 绳,以及戊户 6 绳加甲户 1 绳都恰好等于井深,问井深和各户绳长各几何?

《张丘建算经》上记载的”百鸡问题“.
古文: 今有鸡翁一,值钱五; 鸡母一,值钱三;鸡雏三,值钱一.凡百钱买鸡百只.问鸡翁、母、雏各几何?
现代文:公鸡一只值钱五,母鸡一只值钱三,小鸡三只值钱一.今有一百钱,买鸡一百只,问公鸡、母鸡、小鸡各买几只?

抽屉原理(也被称作鸽巢原理)。将 $n+1$ 个物体,放入$n$个抽屉里,那么有至少一个抽屉有两个(或以上)的物体。这个定理看起来比较显然,证明方法考虑反证法:假如每个分组有至多 $1$ 个物体,那么最多有 $1\times n$ 个物体,而实际上有 $n+1$ 个物体,矛盾。

例如:桌上有5个苹果,要把这5个苹果放到4个抽屉里,无论怎样放,我们会发现至少会有一个抽屉里面放不少于2个苹果。这一现象就是我们所说的“抽屉原理”。 抽屉原理的一般含义为:“如果每个抽屉代表一个集合,每一个苹果就可以代表一个元素,假如有n+1个元素放到n个集合中去,其中必定有一个集合里至少有两个元素。”, 同理 将 $n$ 个物体,划分为 $k$ 组,那么至少存在一个分组,含有大于或等于 $\left \lceil \dfrac{n}{k} \right \rceil$ 个物品。
问题:有300人到招聘会求职,其中软件设计有100人,市场营销有80人,财务管理有70人,人力资源管理有50人。那么至少有多少人找到工作才能保证一定有70人找的工作专业相同呢?
在高中,我们学过了阶乘,其定义为 $ n!= 1 *2*3 \cdot \cdot \cdot n$, 这里$n$为0或者正整数,其中规定 $0!=1$, 例如 $5!=1*2*3*4*5=120$ , 那么你知道 $(\dfrac{1}{2})!$ 是多少吗?