解答题 (共 15 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
设 $f(x)$ 在 $[0,1]$ 上连续,在 $(0,1)$ 内可导,且 $f(0)=0, f(1)=1$ .证明:(1)存在两个不同的点 $\xi_1, \xi_2 \in(0,1)$ ,使得 $f^{\prime}\left(\xi_1\right)+f^{\prime}\left(\xi_2\right)=2$ ;
(2)存在 $\xi, \eta \in(0,1)$ ,使得 $\eta f^{\prime}(\xi)=f(\eta) f^{\prime}(\eta)$ .
(1)设非负连续函数 $f(x)$ 满足 $f(x) \int_0^x f(x-t) d t=\sin ^4 x$ ,求 $f(x)$ 在 $\left[0, \frac{\pi}{2}\right]$ 上的平均值;
(2)(浙江省 2002 年竞赛题)设连续函数 $f(x)$ 在 $(-1,+\infty)$ 内满足 $f(x)\left[\int_0^x f(t) d t+1\right]=\frac{x e ^x}{2(1+x)^2}$ ,求 $f(x)$ .
设函数 $f(x)$ 在 $[a, b]$ 上可导,且
$$
f^{\prime}(a)(b-a) < f(b)-f(a) < 2\left[f\left(\frac{a+b}{2}\right)-f(a)\right] .
$$
(1)记 $F(x)=\frac{f(x)-f(a)}{x-a}-\frac{f(b)-f(a)}{b-a}$ ,证明:存在 $x_0 \in(a, b)$ ,使得 $F\left(x_0\right)=$ 0;
(2)证明:存在 $\xi \in(a, b)$ ,使得 $f^{\prime}(\xi)=\frac{f(\xi)-f(a)}{\xi-a}$ .
设 $f(x)$ 在 $(0,1)$ 内可导,证明 $f(x)$ 的任何两个不同的零点之间一定有函数 $f(x)+f^{\prime}(x)$ 的一个零点,并由此证明方程 $x \ln (1+x)+\frac{x-1}{x+1}=0$ 在 $(0,1)$ 内有且仅有一个实数根.
设 $F(x)=-\frac{1}{2}\left(1+ e ^{-1}\right)+\int_{-1}^1|x-t| e ^{-t^2} d t$ ,求证:在区间 $(-1,1)$ 内,$F(x)$ 有且仅有两个实根.
设存在二元函数 $g(x, y)=f\left( e ^{x y}, x^2+y^2\right)$ ,且 $\lim _{\substack{x \rightarrow 1 \\ y \rightarrow 0}} \frac{f(x, y)+x+y-1}{\sqrt{(x-1)^2+y^2}}=0$ ,证明:$g(x, y)$ 在 $(0,0)$ 处取极值,并求出其极值.
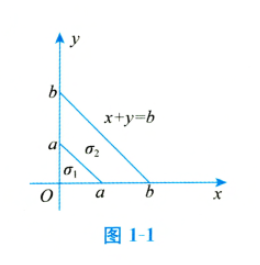
设一薄板平面区域 $\sigma$ 由 $\sigma_1$ 与 $\sigma_2$ 组成,其中,$\sigma_1=\{(x, y) \mid 0 \leqslant y \leqslant a-x, 0 \leqslant x \leqslant a\}, \sigma_2=\{(x, y) \mid a \leqslant x+y \leqslant b$ , $x \geqslant 0, y \geqslant 0\}$ ,如图 1-1 所示.它的面密度
$$
\mu(x, y)= \begin{cases}e^{-(x+y)}, & (x, y) \in \sigma_1, \\ \frac{1}{\sqrt{x^2+y^2}}, & (x, y) \in \sigma_2 .\end{cases}
$$
试求:
(1)该薄板 $\sigma$ 的质量 $m$ ;
(2)薄板 $\sigma_1$ 关于 $y$ 轴的转动惯量 $J_1$ 与 $\sigma_2$ 关于原点的转动惯量 $J_2$ .
设函数 $f(x, y)$ 可微,$\frac{\partial f}{\partial x}=-f(x, y), f\left(0, \frac{\pi}{2}\right)=1$ ,且 满 足 $\lim _{n \rightarrow \infty}\left[\frac{f\left(0, y+\frac{1}{n}\right)}{f(0, y)}\right]^n= e ^{\cot y}$ ,求 $f(x, y)$ .
试求函数 $f(x, y)=1-6 x+3 y+4 x^2+18\left|x^2+y^2-4\right|$ 在平面区域 $\sigma=\{(x$ , y) $\left.\mid x^2+y^2 \leqslant 9\right\}$ 上的平均值.
设 $z=z(x, y)$ 存在二阶连续的偏导数,且 $z(x, y) \neq 0$ ,证明:$z(x, y)= f(x) g(y)$ 的充分必要条件是 $z(x, y) \frac{\partial^2 z}{\partial x \partial y}=\frac{\partial z}{\partial x} \frac{\partial z}{\partial y}$ .
设 $f(x)$ 在 $[1,+\infty)$ 上有连续的二阶导数,$f(1)=0, f^{\prime}(1)=1, z=\left(x^2+\right. \left.y^2\right) f\left(x^2+y^2\right)$ 满足
$$
\frac{\partial^2 z}{\partial x^2}+\frac{\partial^2 z}{\partial y^2}=0
$$
求:(1)$f(x)$ 的表达式;
(2)$f(x)$ 在 $[1,+\infty)$ 上的最大值;
(3)$f(x)$ 的拐点和渐近线;
(4)在 $1, \sqrt{2}, \sqrt[3]{3}, \sqrt[4]{4}, \cdots, \sqrt[n]{n}$ 中,求出最大一个数;
(5)求证:当 $e < x_1 < x_2$ 时,$\frac{x_1}{x_2} < \frac{\ln x_1}{\ln x_2} < \frac{x_2}{x_1}$ ;
(6)$y=f(x)(x \geqslant 1)$ 绕 $x$ 轴旋转一周形成的体积 $V$ .
在第一卦限内作椭球面 $\frac{x^2}{a^2}+\frac{y^2}{b^2}+\frac{z^2}{c^2}=1$ 的切平面,使切平面与三坐标面所围成的四面体体积最小,求切点的坐标.
计算二重积分 $\iint_D \frac{1-x^3 y^2}{\left(y+2 \sqrt{1-x^2}\right)^2} d x d y$ ,其中 $D: x^2+y^2 \leqslant 1,-y \leqslant x \leqslant y$ .
设数列 $a_n=\int_0^1 \frac{x^n}{1+x} d x$ .
(1)证明:$\frac{1}{2(n+1)} \leqslant a_n \leqslant \frac{1}{2 n}, n=1,2, \cdots$ ;
(2)讨论级数 $\sum_{n=1}^{\infty}(-1)^{n-1}\left(\frac{1}{2 n}-\int_0^1 \frac{x^n}{1+x} d x\right)$ 的敛散性,若收敛,请说明是条件收敛还是绝对收敛.
(1)先讨论级数 $\sum_{n=1}^{\infty}\left[\frac{1}{n}-\ln \left(1+\frac{1}{n}\right)\right]$ 的敛散性,又已知 $x_n=1+\frac{1}{2}+\cdots+\frac{1}{n}- \ln (1+n)$ ,证明数列 $\left\{x_n\right\}$ 收敛;
(2)求 $\lim _{n \rightarrow \infty} \frac{1}{\ln n}\left(1+\frac{1}{2}+\cdots+\frac{1}{n}\right)$ .