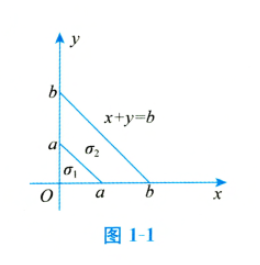
设一薄板平面区域 $\sigma$ 由 $\sigma_1$ 与 $\sigma_2$ 组成，其中，$\sigma_1=\{(x, y) \mid 0 \leqslant y \leqslant a-x, 0 \leqslant x \leqslant a\}, \sigma_2=\{(x, y) \mid a \leqslant x+y \leqslant b$ ， $x \geqslant 0, y \geqslant 0\}$ ，如图 1－1 所示．它的面密度

$$
\mu(x, y)= \begin{cases}e^{-(x+y)}, & (x, y) \in \sigma_1, \\ \frac{1}{\sqrt{x^2+y^2}}, & (x, y) \in \sigma_2 .\end{cases}
$$


试求：
（1）该薄板 $\sigma$ 的质量 $m$ ；
（2）薄板 $\sigma_1$ 关于 $y$ 轴的转动惯量 $J_1$ 与 $\sigma_2$ 关于原点的转动惯量 $J_2$ ．