单选题 (共 12 题 ),每题只有一个选项正确
$5$ 的倒数是 $(\quad)$
$\text{A.}$ $\frac{1}{5}$
$\text{B.}$ $-\frac{1}{5}$
$\text{C.}$ $5$
$\text{D.}$ $-5$
下列各数中为无理数的是 ( )
$\text{A.}$ $\sqrt{2}$
$\text{B.}$ $1.5$
$\text{C.}$ $0$
$\text{D.}$ $-1$
今年我市高中计划招生 52300 人, 将数据 52300 用科学记数法表示是 ( )
$\text{A.}$ $0.523 \times 10^5$
$\text{B.}$ $5.23 \times 10^3$
$\text{C.}$ $5.23 \times 10^4$
$\text{D.}$ $52.3 \times 10^3$
如图, 从热气球 $A$ 看一栋楼底部 $C$ 的俯角是 ( )
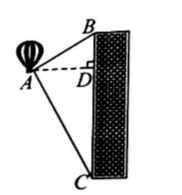
$\text{A.}$ $\angle B A D$
$\text{B.}$ $\angle A C B$
$\text{C.}$ $\angle B A C$
$\text{D.}$ $\angle D A C$
请你量一量如图 $\triangle A B C$ 中 $B C$ 边上的高的长度, 下列最接近的是 ( )

$\text{A.}$ $0.5 \mathrm{~cm}$
$\text{B.}$ $0.7 \mathrm{~cm}$
$\text{C.}$ $1.5 \mathrm{~cm}$
$\text{D.}$ $2 \mathrm{~cm}$
垃圾分类利国利民, 某校宣传小组就“空矿泉水瓶应投放到哪种颜色的垃圾收集桶内”进行统计活动, 他 们随机采访 50 名学生并作好记录. 以下是排乱的统计步骤:
(1)从扇形统计图中分析出本校学生对空矿泉水瓶投放的正确率
(2)整理采访记录并绘制空矿泉水瓶投放频数分布表
(3)绘制扇形统计图来表示空矿泉水瓶投放各收集桶所占的百分比
正确统计步骤的顺序应该是()
$\text{A.}$ (2) $\rightarrow$ (3) $\rightarrow$ (1)
$\text{B.}$ (2) $\rightarrow$ (1) $\rightarrow$ (3)
$\text{C.}$ (3) $\rightarrow$ (1) $\rightarrow$ (2)
$\text{D.}$ (3) $\rightarrow$ (2) $\rightarrow$ (1)
若 $x$ 是非负整数, 则表示 $\frac{2 x}{x+2}-\frac{x^2-4}{(x+2)^2}$ 的值的对应点落在下图数轴上的范围是 ( )
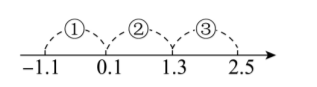
$\text{A.}$ ①
$\text{B.}$ ②
$\text{C.}$ ③
$\text{D.}$ ①或②
龟兔赛跑之后, 输了比赛 兔子决定和乌龟再赛一场. 图中的函数图象表示了龟兔再次赛跑的过程 $(x$ 表示兔子和乌龟从起点出发所走的时间, $y_1, y_2$ 分别表示兔子与乌龟所走的路程). 下列说法错误的是 ( )
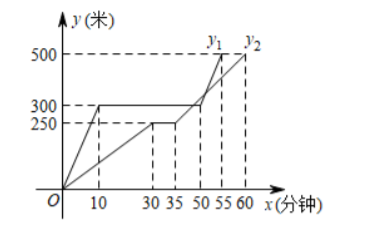
$\text{A.}$ 兔子和乌龟比赛路程是 500 米
$\text{B.}$ 中途, 兔子比乌龟多休息了 35 分钟
$\text{C.}$ 兔子比乌龟多走了 50 米
$\text{D.}$ 比赛结果, 兔子比乌龟早 5 分钟到达终点
若顺次连接四边形 $A B C D$ 各边的中点所得的四边形是正方形, 则四边形 $A B C D$ 的两条对角线 $A C, B D$ 一定是 ( )
$\text{A.}$ 互相平分
$\text{B.}$ 互相垂直
$\text{C.}$ 互相平分且相等
$\text{D.}$ 互相垂直且相等
小嘉说: 将二次函数 $y=x^2$ 的图象平移或翻折后经过点 $(2,0)$ 有 4 种方法:
(1)向右平移 2 个单位长度
(2)向右平移 1 个单位长度, 再向下平移 1 个单位长度
(3)向下平移 4 个单位长度
(4)沿 $x$ 轴翻折, 再向上平移 4 个单位长度
你认为小嘉说的方法中正确的个数有()
$\text{A.}$ 1个
$\text{B.}$ 2个
$\text{C.}$ 3个
$\text{D.}$ 4个
如图的电子装置中, 红黑两枚跳棋开始放置在边长为 2 的正六边形 $A B C D E F$ 的顶点 $A$ 处. 两枚跳棋 跳动规则是: 红跳棋按顺时针方向 1 秒钟跳 1 个顶点, 黑跳棋按逆时针方向 3 秒钟跳 1 个顶点, 两枚跳棋 同时跳动, 经过 2022 秒钟后, 两枚跳棋之间的距离是 ( )

$\text{A.}$ 4
$\text{B.}$ $2 \sqrt{3}$
$\text{C.}$ 2
$\text{D.}$ 0
填空题 (共 6 题 ),请把答案直接填写在答题纸上
已知 $\angle \alpha=60^{\circ}$, 则 $\angle \alpha$ 的余角等于 ( ) 度。
数学课上, 老师将如图边长为 1 的正方形铁丝框变形成以 $A$ 为圆心, $A B$ 为半径的扇形 (铁丝的粗细 忽略不计), 则所得扇形 $D A B$ 的面积是
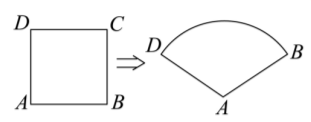
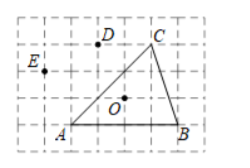
如图, 在 $5 \times 7$ 网格中, 各小正方形边长均为 1 , 点 $O, A, B, C, D, E$ 均在格点上, 点 $O$ 是 $\triangle A B C$ 的 外心, 在不添加其他字母的情况下, 则除 $\triangle A B C$ 外把你认为外心也是 $O$ 的三角形都写出来
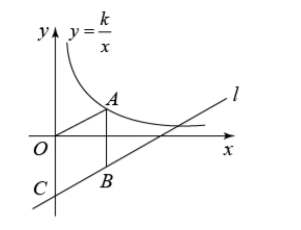
如图, 点 $A$ 在双曲线 $y=\frac{k}{x}(k>0, x>0)$ 上, 点 $B$ 在直线 $y=m x-2 b(m>0, b>0)$ 上, $A$ 与 $B$ 关于 $x$ 轴 对称, 直线 $l$ 与 $y$ 轴交于点 $C$, 当四边形 $A O C B$ 是菱形时, 有以下结论:
(1) $A(b, \sqrt{3} b)$
(2)当 $b=2$ 时, $k=4 \sqrt{3}$
(3) $m=\frac{\sqrt{3}}{3}$
(4) $S_{\text {四边形 } A O C B}=2 b^2$
则所有正确结论的序号是
解答题 (共 8 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
计算: $2022^{\circ}+\sqrt{4}+\left|-\frac{1}{2}\right|-\sin 30^{\circ}$.
解方程: $\frac{x}{x-1}=\frac{x-1}{2 x-2}$.
问题情境:
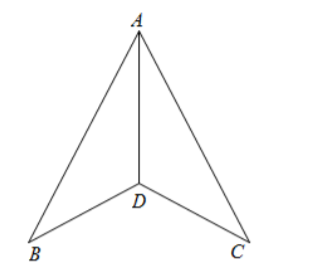
在数学探究活动中, 老师给出了如图的图形及下面三个等式:
①$A B=A C$
②$D B=D C$
③$\angle B A D=\angle C A D$ 若以其中两个等式作为已知条件, 能否得到余下一个等式成立? 解决方案:探究 $\triangle A B D$ 与 $\triangle A C D$ 全等.
问题解决:
(1) 当选择①②作为已知条件时, $\triangle A B D$ 与 $\triangle A C D$ 全等吗? (填 “全等” 或 “不全. 理由是
(2) 当任意选择两个等式作为已知条件时, 请用画树状图法或列表法求 $\triangle A B D \cong \triangle A C D$ 的概率.
为了加强对青少年防溺水安全教育, 5 月底某校开展了 “远离溺水, 珍爱生命” 的防溺水安全知识比 赛. 下面是从参赛学生中随机收集到的 20 名学生的成绩 (单位: 分):
$\begin{array}{llllllllll}87 & 99 & 86 & 89 & 91 & 91 & 95 & 96 & 87 & 97\end{array}$
$\begin{array}{llllllllll}91 & 97 & 96 & 86 & 96 & 89 & 100 & 91 & 99 & 97\end{array}$
整理数据:

分析数据

解决问题
(1) 直接写出上面表格中的 $a, b, c, d$ 的值;
(2) 若成绩达到 95 分及以上为 “优秀” 等级, 求 “优秀” 等级所占的百分率;
(3) 请估计该校 1500 名学生中成绩达到 95 分及以上的学生人数.
如图, $A B$ 是 $\odot O$ 的直径, $C, D$ 都是 $\odot O$ 上的点, $A D$ 平分 $\angle C A B$, 过点 $D$ 作 $A C$ 的垂线交 $A C$ 的 延长线于点 $E$, 交 $A B$ 的延长线于点 $F$.
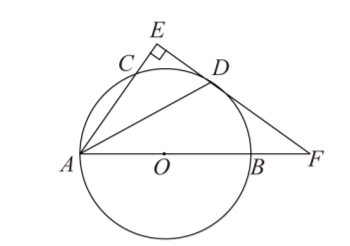
(1) 求证: $E F$ 是 $\odot O$ 的切线;
(2) 若 $A B=10, A C=6$, 求 $\tan \angle D A B$ 的值.
我市某乡村振兴果蔬加工公司先后两次购买龙眼共 21 吨, 第一次购买龙眼的价格为 $0.4$ 万元/吨: 因龙 眼大量上市, 价格下跌, 第二次购买龙眼的价格为 $0.3$ 万元/吨, 两次购买龙眼共用了 7 万元.
(1)求两次购买龙眼各是多少吨?
(2)公司把两次购买的龙眼加工成桂圆肉和龙眼千, 1 吨龙眼可加工成桂圆肉 $0.2$ 吨或龙眼干 $0.5$ 吨, 桂 圆肉和龙眼干的销售价格分别是 10 万元/吨和 3 万元/吨, 若全部的销售额不少于 39 万元, 则至少需要把多 少吨龙眼加工成桂圆肉?
如图, 在矩形 $A B C D$ 中, $A B=8, A D=4$, 点 $E$ 是 $D C$ 边上的任一点 (不包括端点 $D, C$ ), 过点 $A$ 作 $A F \perp A E$ 交 $C B$ 的延长线于点 $F$, 设 $D E=a$.
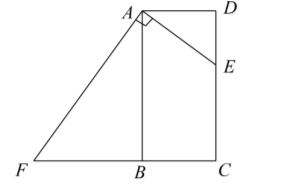
(1) 求 $B F$ 的长 (用含 $a$ 的代数式表示);
(2) 连接 $E F$ 交 $A B$ 于点 $G$, 连接 $G C$, 当 $G C / / A E$ 时, 求证: 四边形 $A G C E$ 是菱形.
如图, 已知抛物线: $y=-2 x^2+b x+c$ 与 $x$ 轴交于点 $A, B(2,0)$ ( $A$ 在 $B$ 的左侧), 与 $y$ 轴交于点 $C$, 对称轴是直线 $x=\frac{1}{2}, P$ 是第一象限内抛物线上的任一点.
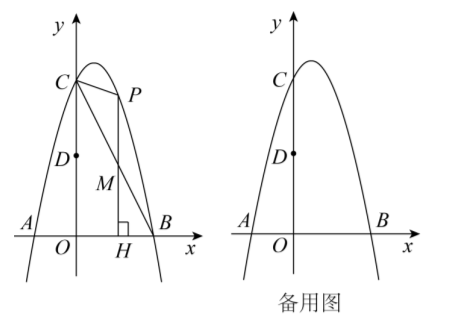
(1) 求抛物线的解析式;
(2) 若点 $D$ 为线段 $O C$ 的中点, 则 $\triangle P O D$ 能否是等边三角形? 请说明理由;
(3) 过点 $P$ 作 $x$ 轴的垂线与线段 $B C$ 交于点 $M$, 垂足为点 $H$, 若以 $P, M, C$ 为顶点的三角形与 $\triangle B M H$ 相似, 求点 $P$ 的坐标.