问题情境:
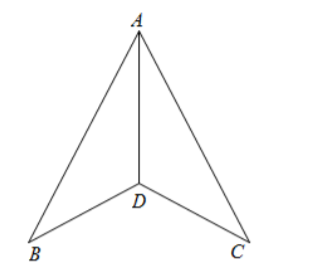
在数学探究活动中, 老师给出了如图的图形及下面三个等式:
①$A B=A C$
②$D B=D C$
③$\angle B A D=\angle C A D$ 若以其中两个等式作为已知条件, 能否得到余下一个等式成立? 解决方案：探究 $\triangle A B D$ 与 $\triangle A C D$ 全等.


问题解决:
(1) 当选择①②作为已知条件时, $\triangle A B D$ 与 $\triangle A C D$ 全等吗? (填 “全等” 或 “不全. 理由是
(2) 当任意选择两个等式作为已知条件时, 请用画树状图法或列表法求 $\triangle A B D \cong \triangle A C D$ 的概率.