单选题 （共 8 题 ），每题只有一个选项正确
已知集合 $A=\{x \in \mathrm{Z} \| x \mid < 3\}, B=(-\infty, 0] \mathrm{U}(1,+\infty)$, 则 $A$ I $B=$ （ ）
$\text{A.}$ $\{-2,-1,0,2\}$
$\text{B.}$ $\{-2,-1,0,1,2\}$
$\text{C.}$ $(-3,0] \cup[1,3)$
$\text{D.}$ $(-3,0] \mathrm{U}(1,3)$
下列函数是偶函数且在 $(0,+\infty)$ 上单调递增的是 ( )
$\text{A.}$ $f(x)=\sqrt[2]{x^3}$
$\text{B.}$ $f(x)=\frac{\mathrm{e}^x-\mathrm{e}^{-x}}{2}$
$\text{C.}$ $f(x)=\left|2^x-1\right|$
$\text{D.}$ $f(x)=|x| x^2$
已知函数 $y=x^2-2 x+2$ 在区间 $[a, b]$ 上的值域是 $[1,2]$ ，则区间 $[a, b]$ 可能是 ( )
$\text{A.}$ $[-1,0]$
$\text{B.}$ $\left[0, \frac{3}{2}\right]$
$\text{C.}$ $[1,3]$
$\text{D.}$ $[-1,1]$
设 $a, b, c$ 均为不等于 1 的正实数，则下列等式中恒成立的是（）
$\text{A.}$ $\log _c a+\log _c b=\log _c(a+b)$
$\text{B.}$ $\log _c a+\log _b c=\log _b a$
$\text{C.}$ $\log _c a \log _c b=\log _c(a+b)$
$\text{D.}$ $\log _b c \log _c a=\log _b a$
函数 $f(x)=\left|\frac{x+1}{x-1}\right|$ 的图象可能是
$\text{A.}$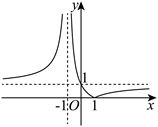 
$\text{B.}$ 
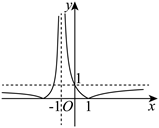$\text{C.}$ 
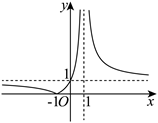$\text{D.}$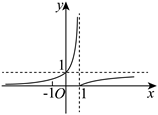 
设定义在 R 上函数 $y=f(x)$ 满足 $y=f(x+2)$ 为偶函数， $y=f(x-1)$ 为奇函数， $f(3)=1$ ，则 $f(13)=(\quad)$
$\text{A.}$ -1
$\text{B.}$ 0
$\text{C.}$ 1
$\text{D.}$ 3
已知 $a, b \in \mathbf{R}$, 则 $a < b$ 是 $a < |b|$ 的（）条件
$\text{A.}$ 充分不必要
$\text{B.}$ 充分必要
$\text{C.}$ 必要不充分
$\text{D.}$ 既不充分也不必要
已知函数 $f(x)=a \cdot 4^x-(a-2) 2^x+1$ 在 $(-2,+\infty)$ 上单调递增, 则 $a$ 的取值范围为 $(\quad)$
$\text{A.}$ $[0,4]$
$\text{B.}$ $(0,4]$
$\text{C.}$ $[2,+\infty)$
$\text{D.}$ $\{0\} \cup[2,+\infty)$
多选题 （共 4 题 ），每题有多个选项正确
下列命题为真命题的是（）
$\text{A.}$ 若 $a>b$, 则 $a c^2 \geq b c^2$
$\text{B.}$ 若 $a>b$, 则 $\sqrt[3]{a^2}>\sqrt[3]{b^2}$
$\text{C.}$ 若 $a>b>0, m>0$, 则 $\frac{b+m}{a+m}>\frac{b}{a}$
$\text{D.}$ 若 $a b>0, \frac{1}{a} < \frac{1}{b}$, 则 $a^2>b^2$
下列命题是真命题的是（）
$\text{A.}$ 若 $\left(\frac{1}{2}\right)^x>1>4^y$, 则 $x+2 y < 0$
$\text{B.}$ 若 $f(x+2)$ 的定义域为 $[0,2]$, 则 $y=f(x)$ 的定义域为 $[-2,0]$ ；
$\text{C.}$ 函数 $y=\left\{\begin{array}{l}x(4-x), x \geq 0 \\ x(4+x), x < 0\end{array}\right.$ 是定义在 $\mathbf{R}$ 上的单调递增奇函数
$\text{D.}$ 记 $\min \{a, b\}$ 为实数 $a, b$ 的最小值, $\max \{a, b\}$ 为实数 $a, b$ 的最大值, 函数 $f_1(x)=x^2$, $f_2(x)=-x^2+4 x, f(x)=\min \left\{f_1(x), f_2(x)\right\}, g(x)=\max \left\{f_1(x), f_2(x)\right\}$ ，则 $f(x)$ 的最大值与 $g(x)$ 的最小值的差为 4 .
已知函数 $y=f(x)$ 的图象关于 $P(a, b)$ 成中心对称图形的充要条件是 $y=f(x+a)-b$ 是奇函数，函数 $y=f(x)$ 的图象关于 $x=a$ 成轴对称图形的充要条件是 $y=f(x+a)$ 是偶函数. 则下列说法正确的是（）
$\text{A.}$ $f(x)=x^3-3 x^2$ 的对称中心为 $(1,-2)$
$\text{B.}$ $f(x)=x^4-4 x^3+6 x^2-4 x$ 关于 $x=1$ 对称
$\text{C.}$ $f(x)=\frac{2 x+1}{x-1}$ 的对称中心为 $(1,-2)$
$\text{D.}$ $f(x)=\frac{x-2}{x^2-4 x+5}$ 的图象关于 $(-2,0)$ 对称
已知实数 $a, b$ 满足 $a^2+4 b^2-a b=1$, 则下列结论正确的是 ( )
$\text{A.}$ $a^2+4 b^2$ 的最大值为 $\frac{4}{3}$
$\text{B.}$ $a^2+4 b^2$ 的最大值为 2
$\text{C.}$ $a+2 b$ 的最小值为 $\frac{2 \sqrt{6}}{3}$
$\text{D.}$ $a+b$ 的最小值为 $-\frac{2 \sqrt{10}}{5}$
填空题 （共 4 题 ），请把答案直接填写在答题纸上
命题" $\exists x>3, x^2-5 < 0$ "的否定是
已知 $\log _2 a+\log _2 b=\log _2 \frac{9}{2}$, 则 $3^a+9^b$ 的最小值为
己知某种果蔬的有效保鲜时间 $y$ （单位：小时）与储藏温度 $x$ （单位： ${ }^{\circ} \mathrm{C}$ ）近似满足函数关系 $y=\mathrm{e}^{a x+b}$ （ $a, b$ 为常数， e 为自然对数底数），若该果蔬在 $4^{\circ} \mathrm{C}$ 的保鲜时间为 216 小时，在 $16^{\circ} \mathrm{C}$ 的有效保鲜时间为 8 小时, 那么在 $8^{\circ} \mathrm{C}$ 时, 该果蔬的有效保鲜时间大约为 $\qquad$ 小时.
已知函数 $f(x)=\left\{\begin{array}{l}x^2-x+4, x \leq 1, \\ x+\frac{3}{x}, x>1 .\end{array}\right.$ 设 $a \in \mathbf{R}$, 若关于 $x$ 的不等式 $f(x) \geq\left|\frac{x}{2}+a\right|$ 在 $\mathbf{R}$ 上恒成立,则 $a$ 的取值范围是 .
解答题 （共 6 题 ），解答过程应写出必要的文字说明、证明过程或演算步骤
求值
(1) $(-1)^0+\sqrt[4]{\left(-\frac{1}{2}\right)^4}+4 a^{\frac{2}{3}} b^{-\frac{1}{3}} \div\left(-\frac{2}{3} a^{-\frac{1}{3}} b^{-\frac{1}{3}}\right)$
(2)已知 $\lg 3=m, \lg 5=n$, 用 $m, n$ 表示 $\log _4 6$.
已知关于 $x$ 的方程 $a x^2-a x+1=0$ 有实根, 集合 $B=\{x| | x-6 \mid < m\}$.
(1)求 $a$ 的取值集合 A ;
(2)若 $A \cap B=B$, 求 $m$ 的取值范围.
定义 $\mathbf{R}$ 上的函数 $f(x)$ 为奇函数, $g(x)$ 为偶函数, $f(x)+g(x)=2^{x+1}-1$.
(1) 求函数 $f(x) 、 g(x)$ 的解析式;
(2)判断并证明 $g(x)$ 的单调性.
已知 $x$ 为实数, 用 $[x]$ 表示不超过 $x$ 的最大整数.
(1) 若函数 $f(x)=[x]$, 求 $f(2.5), f\left(2^{\frac{1}{3}}\right)$ 的值;
(2) 若存在 $2 < m < 3$, 使得 $f(m)=f([m])$, 则称函数 $f(x)$ 是 $2 \Omega$ 函数, 若函数 $f(x)=x+\frac{a}{x}$ 是
$2 \Omega$ 函数, 求 $a$ 的取值范围.
已知函数 $f(x)=\frac{2 g(x)(g(2 x)+1)}{(2 g(2 x)+1)(g(2 x)+2)}, g(x)=e^x, h(x)=e^{2 x}+\left|e^x-a\right|, a \in \mathbf{R}$.
(1) 求 $f(x)$ 的解析式并判断其奇偶性;
(2)已知对任意的 $x_1, x_2 \in \mathbf{R}$, 都有 $f\left(x_1\right) \leq h\left(x_2\right)$, 求参数 $a$ 的取值范围.
已知定义域为 $D$ 的函数 $f(x)$, 若存在实数 $a$, 使得 $\forall x_1 \in D$, 都存在 $x_2 \in D$ 满足 $\frac{x_1+f\left(x_2\right)}{2}=a$,则称函数 $f(x)$ 具有性质 $P(a)$.
(1) 判断函数 $f(x)=3^x$ 是否具有性质 $P(0), g(x)=x^3$ 是否具有性质 $P(1)$, 说明理由;
(2) 若存在唯一实数 $a$, 使得函数 $f(x)=t x^2+x+4, x \in[0,4]$ 具有性质 $P(a)$, 求实数 $t$ 的值.