单选题 (共 7 题 ),每题只有一个选项正确
如图甲所示, 让绳穿过一块带有狭缝的木板, 当狭缝与振动方向垂直放置时, 绳波不能穿过狭缝; 如图 乙所示, 在一条弹簧上传播的波, 无论狭缝取向如何, 波都能穿过. 下列说法正确的是

$\text{A.}$ 横波各点振动方向与波传播方向共线, 纵波各点振动方向与波传播方向垂直
$\text{B.}$ 不同的横波,即使传播方向相同, 振动 方向也可能不同,这个现象叫偏振现象甲
$\text{C.}$ 甲、乙两图说明, 偏振现象是波的固有属性, 也是纵波特有的现象
$\text{D.}$ 光也有偏振现象, 当光的偏振方向与透振方向垂直时, 透射光的强度比较大
如图所示, $M N$ 是一圆的直径, 在圆形区域内, $M N$ 的左、右两侧存在方向分别垂直纸面向里、向外的匀 强磁场, 磁感应强度大小分别为 $B 、 2 B$; 将由三段粗细相同的同一材料的导体所构成的正三角形 $a b c$ 置 于圆形平面内, 其中 $c$ 与 $M$ 重合、 $N$ 为圆与 $a b$ 边相切的切点; 再将正三角形的 $a 、 c$ 两点接人电路, 电路 中的电流由 $a$ 流人三角形、由 $c$ 流出, 大小为 $I$. 已知正三角形的边长为 $L$, 则正三角形 $a b c$ 受到的安培 力大小为
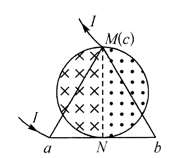
$\text{A.}$ $BIL$
$\text{B.}$ $\frac{1}{2} B I L$
$\text{C.}$ $\frac{1}{3} B I L$
$\text{D.}$ $\frac{1}{4} B I L$
如图所示, 质量为 $m$ 的探测器被火星捕获后绕火星做匀速圆周运动, 当探测器运行到 $A$ 点的瞬间, 同 时发射两束激光,一束激光经过时间 $t$ 到达火星表面的 $B$ 点, 另一束激光经过时间 $2 t$ 到达火星表面的$C$ 点, $B$ 点是火星表面距 $A$ 点最近的点, $C$ 点与 $A$ 点的连线与火星表面相切, 已知火星表面的重力加速$g_火$,引力常量为$G$,激光的速度为$c$,不考虑火星的自转,下列说法正确的是
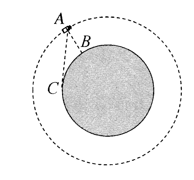
$\text{A.}$ 探测器绕火星运行的轨道半径为 $\frac{7}{2} c t$
$\text{B.}$ 火星的半径为 $\frac{5}{2} c t$
$\text{C.}$ 火星的质量为 $\frac{9 g \text { 火 } c^2 t^2}{4 G}$
$\text{D.}$ 由题设条件不能确定火星的第一宇宙速度
某种理想气体, 从状态 $A$ 到状态 $B$ 、到状态 $C$ 、再回到状态 $A$, 其压强 $p$ 与体积的倒数 $V^{-1}$ 的关系图像 如图所示, $A B$ 的反向延长线经过坐标原点 $O, B C$ 与横轴平行, 下列说法正确的是

$\text{A.}$ 气体从状态 $A$ 到状态 $B$ 做等温变化
$\text{B.}$ 气体从状态 $A$ 到状态 $B$ 从外界吸收热量
$\text{C.}$ 气体从状态 $B$ 到状态 $C$ 做等压升温变化
$\text{D.}$ 气体从状态 $C$ 回到状态 $A$ 温度逐渐降低
如图所示, 长为 $L$ 的绝缘细线的一端连接一个质量为 $m$ 的金属小球 $A$, 另一端固定在一坚直墙壁左边 檐角上的 $O$ 点, 使小球 $A$ 刚好贴着墙壁, 在墙壁上画好一个以 $O$ 为圆心的量角刻度尺; 取一个与 $A$ 完 全相同的小球 $B, B$ 连接绝缘直杆, 绝缘杆另一端也固定于 $O$ 点, 保持绝缘杆坚直. 现让 $A 、 B$ 带上电 荷, 当 $A 、 B$ 平衡时, 发现 $A 、 B$ 的高度相同, 且细线偏离坚直方向的夹角为 $\theta$, 已知重力加速度为 $g$, 下 列说法正确的是
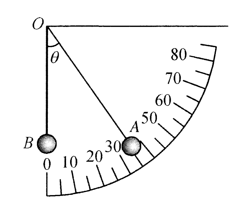
$\text{A.}$ $A 、 B$ 带异种电荷
$\text{B.}$ $A 、 B$ 一定均带正电荷
$\text{C.}$ 细线对 $A$ 的拉力大小为 $\frac{m g}{\sin \theta}$
$\text{D.}$ 绝缘杆对 $B$ 的弹力大小为 $\frac{m g}{\cos \theta}$
真空中相距为 $3 a$ 的两个点电荷 $M 、 N$, 分别固定于 $x$ 轴上 $x_1=0$ 和 $x_2=3 a$ 的两点, 若取 $x$ 轴的正方向 为电场强度的正方向, 则在两者连线上各点的电场强度随 $x$ 变化的关系如图所示. 规定无穷远处电势 为零, 电荷量为 $Q$ 的点电荷在距离其 $r$ 处产生的电势为 $\varphi=\frac{k Q}{r}$, 其中 $k$ 为静电 力常量. 下列说法正确的是
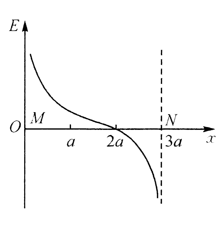
$\text{A.}$ $M 、 N$ 所带电荷量之比为 $Q_M: Q_N=2: 1$
$\text{B.}$ $x=2 a$ 处的电势等于零
$\text{C.}$ 重力不计的带正电粒子 $q$ 可在 $x_3=a$ 和 $x_4=2 \frac{2}{3} a$ 之间做往复运动
$\text{D.}$ 带负电粒子 $-q$ 从 $x=a$ 沿 $x$ 轴正向移动到 $x=2 a$ 的过程中, 电势能减小
如图所示, 小球乙用轻质细线悬挂在 $B$ 点, 在水平面内做匀速圆周运动, 轨迹的圆心为 $O$, 细线与坚直 方向的夹角为 $37^{\circ}$; 现将小球甲从 $A$ 点以向右的初速度 $v_0=5 \mathrm{~m} / \mathrm{s}$ 水平抛出, 正好经过 $O$ 点. 已知 $A 、 B$ 两点的高度差为 $h_{A B}=4.7 \mathrm{~m}, A 、 O$ 两点间的距离为 $s_{A O}=10 \sqrt{5} \mathrm{~m}$, 重力加速度 $g$ 取 $10 \mathrm{~m} / \mathrm{s}^2, \sin 37^{\circ}=0.6. $\cos 37^{\circ}=0.8$, 下列说法正确的是
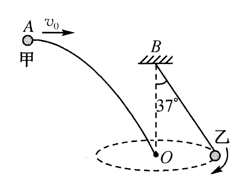
$\text{A.}$ 甲从 $A$ 到 $O$ 的运动时间为 $2 \mathrm{~s}$
$\text{B.}$ $B 、 O$ 两点间的高度差为 $13.3 \mathrm{~m}$
$\text{C.}$ 甲刚好运动到 $O$ 点时, 甲、乙的速率之比为 $5: 4$
$\text{D.}$ 甲刚好运动到 $O$ 点时, 甲、乙的速率之比为 $10: 9$
多选题 (共 4 题 ),每题有多个选项正确
如图所示, 为探究霍尔效应, 取一块长度为 $a$ 、宽度为 $b$ 、厚度为 $d$ 的金属导体, 给金属导体加与前、后面 垂直的匀强磁场 $B$, 通以图示方向的电流 $I$ 时, 规定零电势后, 用电势测量仪测得上、下表面 $M 、 N$ 的电 势分别为 $\varphi_M 、 \varphi_N$, 且 $\varphi_M < \varphi_N$. 已知自由电子的电荷量为 $\mathrm{e}$, 则下列说法正确的是
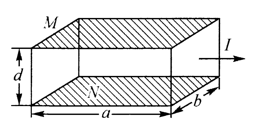
$\text{A.}$ 磁场方向由金属块的前面指向后面
$\text{B.}$ 磁场方向由金属块的后面指向前面
$\text{C.}$ 导体中自由电子定向移动的速度大小为 $v=\frac{\varphi_N-\varphi_M}{B d}$
$\text{D.}$ 导体单位体积内的自由电荷为 $n=\frac{B I}{\mathrm{e} a\left(\varphi_N-\varphi_M\right)}$
如图所示, 理想变压器原线圈两端接电压有效值为 $U_0$ 的交流电压, 副线圈两端接的电动机 $M$ 的内阻 为 $r$, 此时电动机的热功率与消耗的电功率分别为 $P_1 、 P_2$, 在改变电阻箱接人回路阻值的过程中, 元件 都不会烧毁,下列说法正确的是
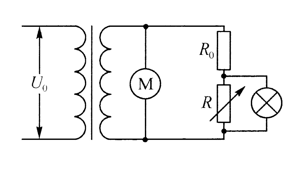
$\text{A.}$ 当电阻箱接人回路的阻值减小时, 灯泡变暗, 流过电动机的电流不变
$\text{B.}$ 变压器原、副线圈匝数比为 $\frac{U_0}{P_2} \sqrt{\frac{P_1}{r}}$
$\text{C.}$ 电动机的效率为 $\frac{P_1}{P_2} \times 100 \%$
$\text{D.}$ 若副线圈两端的电压为 $U$, 电阻箱接人的阻值为 $R$, 则经过 $R_0$ 的电流小于 $\frac{U}{R+R_0}$
静止的重金属原子核 ${ }_{83}^{21} \mathrm{Bi}$ 在磁感应强度为 $B$ 的匀强磁场中发生衰变后, 运动轨迹如图中的 $1 、 2$ 所 示, 已知轨迹 2 对应粒子的动量为 $p$, 带电量为 $q$, 下列说法正确的是
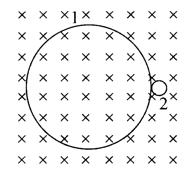
$\text{A.}$ 新核 X 的运动轨迹对应大圆 1
$\text{B.}$ ${ }_{83}^{211} \mathrm{Bi}$ 发生的是 $\alpha$ 衰变
$\text{C.}$ ${ }_{83}^{21} \mathrm{Bi}$ 发生的是 $\beta$ 衰变
$\text{D.}$ 大、小圆对应的半径之差为 $\frac{79 p}{2 B q}$
如图所示, 倾角为 $37^{\circ}$ 的传送带以速度 $v_0$ 逆时针匀速传动, 小滑块 (视为质点) 以平行于传送带的初速 度 $v=2 \mathrm{~m} / \mathrm{s}$ 从顶端滑上传送带, 经过 $t_0=4 \mathrm{~s}$ 滑块滑到传送带的底端, 在此过程中, 滑块的平均速度
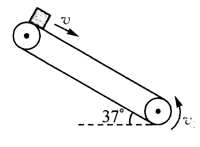
$\text{A.}$ 传送带转轴中心间的距离为 $4 \mathrm{~m}$
$\text{B.}$ 滑块与传送带之间的动摩擦因数为 0.8
$\text{C.}$ 当滑块向上运动到两轮间的中点位置时速度大小正好为 $v_0$, 则滑块在上升过 程中经历的总时间为 $3 \sqrt{2} \mathrm{~s}$
$\text{D.}$ 若 $v_0=v$, 则滑块在传送带上运动的整个过程中, 滑块与传送带的相对位移为 $8 \mathrm{~m}$
填空题 (共 2 题 ),请把答案直接填写在答题纸上
如图所示是一位学生设计的测定自由落体加速度的实验, 在一个敞口容器的底部插人一根细 橡皮管, 并装上一个夹子, 在其下方地面上放一个金属盘子; 调节夹子的松紧, 以使第 1 个水滴落人盘 中发出响声的瞬间, 第 2 个水滴正好从管口落下. 以某次响声为“ 0“开始计数, 待数到“ 100 ”时测得经过的时间为 $40 \mathrm{~s}$, 再用米尺量出管口至盘子的高度为 $78.2 \mathrm{~cm}$. 回答下列问题:
(1) 相邻的两滴水从管口落下的时间间隔为 ________ $T=$ $\mathrm{s}$;
(2) 重力加速度为 $g=$ ________ $\mathrm{m} / \mathrm{s}^2$ (计算结果保留三位有效数字);
(3) 重力加速度的测量结果比当地的重力加速度略 ________ (填“大”或“小”), 原因是空气对 水滴有的作用 ________ .

某同学利用现有的器材设计了如图甲所示的电路图来测量定值电阻 $R_x$ 及电源的电动势 $E$, 如 图乙是所给的实验器材及部分器材连接的电路, 电源的电动势 $E$ 约为 $3 \mathrm{~V}$, 内阻不计; 定值电阻 $R_x$ 的 阻值约为 $300 \Omega$; 电阻箱 $R$ 的阻值范围为 $0 \sim 999.9 \Omega$; 理想电压表的量程范围为 $0 \sim 3 \mathrm{~V}$. 回答下列问 题:
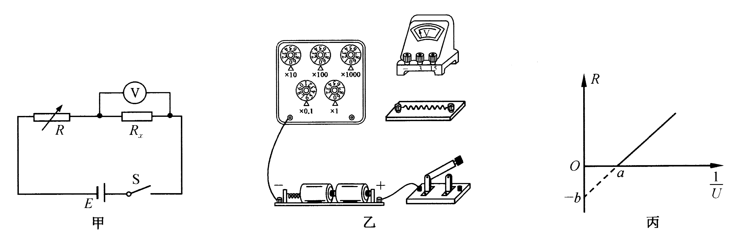
(1) 用笔画线代替导线完成乙图中的器材连接;
(2) 该同学连续调节电阻箱的阻值 $R$, 得到多组 $R$ 和电压表示数 $U$ 的数据, 写出 $R$ 关于 $\frac{1}{U}$ 的函数表达式 为 ________ (用 $E 、 R 、 R_x 、 U$ 表示); 根据数据画出 $R-\frac{1}{U}$ 图线, 如图丙所示, 由图中的数据 $a 、-b$ 可得 定值电阻 $R_x=$ ________ , 电源的电动势 $E=$ ________
解答题 (共 3 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
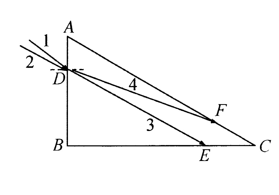
如图所示, 三棱镜的截面为直角三角形, 其中 $A B$ 边与 $B C$ 边垂直, $\angle C=30^{\circ}$, 两束颜色相同的 单色光 $1 、 2$ 从 $A B$ 边上的 $D$ 点射人棱镜, 光线 1 的人射角的正弦值为 $\sin i_1=\frac{\sqrt{6}-\sqrt{2}}{2}$. 其折射光线 3 与 $A C$ 边平行射到 $B C$ 边上的 $E$ 点, 光线 2 的人射角为 $i_2$, 其折射光线 4 射到 $A C$ 边上的 $F$ 点. 正好发 生全发射, $A 、 D$ 两点之间的距离为 $L$, 光在真空中的传播速度为 $c, \sin 75^{\circ}=\frac{\sqrt{6}-\overline{2}}{4}, \sin 15^{\circ}=\frac{\sqrt{6}-\sqrt{2}}{4}$, 求:
(1) 三棱镜对此种颜色光发生全反射时的临界角 $C$;
(2) 光线 4 从 $D$ 到 $F$ 的传播时间.
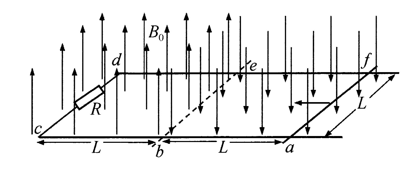
如图所示, 光滑平行、间距为 $L$ 的导轨 $a b c$ 与 $d e f$ 固定在绝缘的水平面上, 在 $c 、 d$ 之间接上定 值电阻, $a 、 f$ 两点的连线, $b 、 e$ 两点的连线, $c 、 d$ 两点的连线均与导轨垂直, $a 、 b$ 两点间的距离, $b 、 c$ 两点 间的距离均为 $L$, 边界 $b e$ 的右侧存在方向坚直向下、磁感应强度随时间按照某种规律变化的匀强磁 场, $b e$ 的左侧存在方向坚直向上、磁感应强度恒为 $B_0$ 的匀强磁场; 现把质量为 $m$ 的导体棒放在 $a 、 f$ 两点上, 计时开始, 方向坚直向下的磁场在初始时刻的磁感应强度为 $B_0$, 此时给导体棒一个水平向左 且与导体棒垂直的速度, 导体棒匀速运动到边界 $b 、 e$ 处, 接着运动到 $c 、 d$ 处速度正好为 0 . 定值电阻的 阻值为 $R$, 其余的电阻均忽略不计, 求:
(1) 导体棒从 $b 、 e$ 处运动到 $c 、 d$ 处, 回路生成的热量;
(2)计时开始, 边界 $b e$ 右侧坚直向下的匀强磁场的磁感应强度 $B$ 随时间 $t$ 变化的关系表达式.
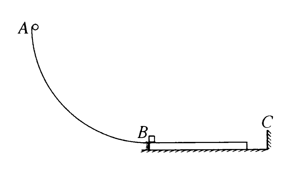
如图所示, 质量为 $m_3=2 \mathrm{~kg}$ 的长木板静止在光滑的水平面上, 其左端与半径为 $r=7.2 \mathrm{~m}$ 的 光滑四分之一圆弧轨道 $A B$ 的最低点 $B$ 接触, 圆弧轨道 $A B$ 固定在坚直平面内, 最低点 $B$ 的切线水平 且 $B$ 点与长木板的上表面等高; 在长木板右侧地面距其右端一定距离处有一坚直固定的挡板 $C$, 质量 为 $m_2$ 的木块 (视为质点) 放置在长木板的左端, 木块与长木板上表面之间的动摩擦因数为 $\mu=0.3$. 现 让质量为 $m_1=0.5 \mathrm{~kg}$ 的小球 (视为质点) 从圆弧轨道最高点 $A$ 由静止释放, 运动到 $B$ 点时与木块正碰 产生的热量为 $Q=18 \mathrm{~J}$, 且小球对木块的冲量为 $I=6 \mathrm{~N} \cdot \mathrm{s}$, 重力加速度 $g$ 取 $10 \mathrm{~m} / \mathrm{s}^2$.
(1)求木块的质量 $m_2$;
(2) 在以后的运动过程中, 若长木板与挡板 $C$ 发生弹性碰撞后, 不再与挡板 $C$ 、圆弧轨道 $A B$ 发生碰 撞, 且木块未从长木板上滑落, 求长木板与挡板 $C$ 发生碰撞时木块的速度及长木板右端到挡板 $C$ 的距离 $s$;
(3) 接第 (2) 问, 当木块与长木板相对静止时, 木块位于长木板的最右端, 求长木板的长度及长木板停 止运动时左端到挡板 $C$ 的距离.