查看原题
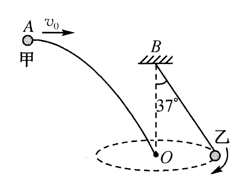
如图所示, 小球乙用轻质细线悬挂在 B 点, 在水平面内做匀速圆周运动, 轨迹的圆心为 O, 细线与坚直 方向的夹角为 37∘; 现将小球甲从 A 点以向右的初速度 v0=5 m/s 水平抛出, 正好经过 O 点. 已知 A、B 两点的高度差为 hAB=4.7 m,A、O 两点间的距离为 sAO=105 m, 重力加速度 g 取 10 m/s2,sin⁡37∘=0.6.\cos 37^{\circ}=0.8$, 下列说法正确的是
A. 甲从 A 到 O 的运动时间为 2 s     B. B、O 两点间的高度差为 13.3 m     C. 甲刚好运动到 O 点时, 甲、乙的速率之比为 5:4     D. 甲刚好运动到 O 点时, 甲、乙的速率之比为 10:9         
不再提醒