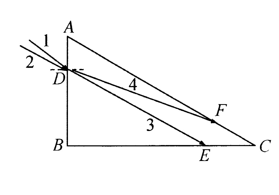
如图所示, 三棱镜的截面为直角三角形, 其中 $A B$ 边与 $B C$ 边垂直, $\angle C=30^{\circ}$, 两束颜色相同的 单色光 $1 、 2$ 从 $A B$ 边上的 $D$ 点射人棱镜, 光线 1 的人射角的正弦值为 $\sin i_1=\frac{\sqrt{6}-\sqrt{2}}{2}$. 其折射光线 3 与 $A C$ 边平行射到 $B C$ 边上的 $E$ 点, 光线 2 的人射角为 $i_2$, 其折射光线 4 射到 $A C$ 边上的 $F$ 点. 正好发 生全发射, $A 、 D$ 两点之间的距离为 $L$, 光在真空中的传播速度为 $c, \sin 75^{\circ}=\frac{\sqrt{6}-\overline{2}}{4}, \sin 15^{\circ}=\frac{\sqrt{6}-\sqrt{2}}{4}$, 求:
(1) 三棱镜对此种颜色光发生全反射时的临界角 $C$;
(2) 光线 4 从 $D$ 到 $F$ 的传播时间.