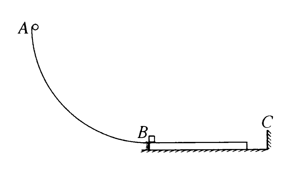
如图所示, 质量为 $m_3=2 \mathrm{~kg}$ 的长木板静止在光滑的水平面上, 其左端与半径为 $r=7.2 \mathrm{~m}$ 的 光滑四分之一圆弧轨道 $A B$ 的最低点 $B$ 接触, 圆弧轨道 $A B$ 固定在坚直平面内, 最低点 $B$ 的切线水平 且 $B$ 点与长木板的上表面等高; 在长木板右侧地面距其右端一定距离处有一坚直固定的挡板 $C$, 质量 为 $m_2$ 的木块 (视为质点) 放置在长木板的左端, 木块与长木板上表面之间的动摩擦因数为 $\mu=0.3$. 现 让质量为 $m_1=0.5 \mathrm{~kg}$ 的小球 (视为质点) 从圆弧轨道最高点 $A$ 由静止释放, 运动到 $B$ 点时与木块正碰 产生的热量为 $Q=18 \mathrm{~J}$, 且小球对木块的冲量为 $I=6 \mathrm{~N} \cdot \mathrm{s}$, 重力加速度 $g$ 取 $10 \mathrm{~m} / \mathrm{s}^2$.
(1)求木块的质量 $m_2$;
(2) 在以后的运动过程中, 若长木板与挡板 $C$ 发生弹性碰撞后, 不再与挡板 $C$ 、圆弧轨道 $A B$ 发生碰 撞, 且木块未从长木板上滑落, 求长木板与挡板 $C$ 发生碰撞时木块的速度及长木板右端到挡板 $C$ 的距离 $s$;
(3) 接第 (2) 问, 当木块与长木板相对静止时, 木块位于长木板的最右端, 求长木板的长度及长木板停 止运动时左端到挡板 $C$ 的距离.
(1)求木块的质量 $m_2$;
(2) 在以后的运动过程中, 若长木板与挡板 $C$ 发生弹性碰撞后, 不再与挡板 $C$ 、圆弧轨道 $A B$ 发生碰 撞, 且木块未从长木板上滑落, 求长木板与挡板 $C$ 发生碰撞时木块的速度及长木板右端到挡板 $C$ 的距离 $s$;
(3) 接第 (2) 问, 当木块与长木板相对静止时, 木块位于长木板的最右端, 求长木板的长度及长木板停 止运动时左端到挡板 $C$ 的距离.
