解答题 (共 8 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
证明: 存在有理数集 $\mathbb{Q}$ 的无限子集 $A$ 和 $B$, 同时满足以下三个条件:
(i) $A \cup B=\mathbb{Q}, A \cap B=\emptyset$;
(ii) $\forall x, y \in A \Rightarrow x y \in B, \forall x, y \in B \Rightarrow x y \in B$;
(iii) $\forall n \in \mathbb{Z},(n, n+1) \cap A \neq \emptyset,(n, n+1) \cap B \neq \emptyset$. (杨晓鸣供题)
设 $a, b, c, d \in(0,1)$, 满足 $a^2+b^2+c^2+d^2=3$. 证明:
$$
\frac{1-a^2}{b+c}+\frac{1-b^2}{c+d}+\frac{1-c^2}{d+a}+\frac{1-d^2}{a+b} < \frac{2}{3} \text {. (李胜宏供题) }
$$
求最大的正整数 $n$, 使得平面上存在 $n$ 个点 $P_1, P_2, \cdots, P_n$ (任意三点不共线) 和不过其中任意点的 $n$ 条直线 $l_1, l_2, \cdots, l_n$ (任意三线不共点), 满足对任意 $i \neq j$,直线 $P_i P_j, l_i, l_j$ 三线共点. (王家军供题)
有红、黄、蓝 3 种不同颜色的帽子各足够多顶. 一个游戏团队有 $n(\geq 4)$ 个人,每人都知晓团队的人数为 $n$ ,帽子的颜色有红、黄、蓝 3 种可能. 他们围成一圈进行如下游戏:
步骤 1:AI 给每个人分配一顶帽子,每人都看不到自己的帽子,只能看到与自己相邻的两人 (即顺时针、逆时针离他最近的人) 的帽子;
步骤 2:所有人同时猜自己的帽子颜色,只要有一个人猜对,就视作游戏团队获胜;若所有人都猜错,则 AI 获胜。
游戏团队可在步骤 1 之前约定猜帽子颜色的策略.
(1) $n=4$ 时,游戏团队是否有必胜策略?证明你的结论;
(2) $n=9999$ 时,游戏团队是否有必胜策略?证明你的结论.(郑文迅供题)
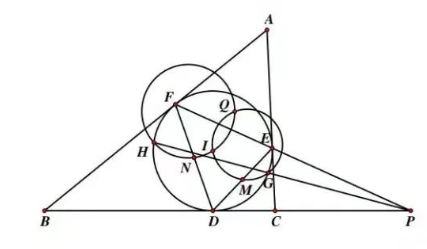
如图, 在 $\triangle A B C$ 中, $A B>A C, \triangle A B C$ 的内切圆 $I$ 分别切边 $B C, C A, A B$ 于点 $D, E, F$. 设 $M$ 为 $D E$ 中点, $N$ 为 $D F$ 中点, 直线 $F E$ 与 $B C$ 相交于点 $P$. 过点 $P$ 作动直线 $l$ 交内切圆 $I$ 于不同的两点 $G, H$, 且 $I, M, G$ 和 $I, N, H$ 均不共线, $\triangle I M G$ 的外接圆与 $\triangle I N H$ 的外接圆交于不同于 $I$ 的一点 $Q$. 证明: 点 $Q$ 始终在一个定圆上. (张惠东供题)
设 $n$ 为正整数. 若平面中存在两点 $A, B$ 及 2024 个不同的点 $P_1, P_2, \cdots, P_{2024}$,满足: 线段 $A B$ 及各条线段 $A P_i, B P_i(i=1,2, \cdots, 2024)$ 的长度均为不超过 $n$ 的正整数, 求 $n$ 的最小值. (何忆捷供题)
设 $m, n$ 为正整数且 $m \leq n$, 证明:
$$
\left|\sum_{k=m}^n\left(\cos \frac{k^2 \pi}{2 n}+i \sin \frac{k^2 \pi}{2 n}\right)\right| \leq \frac{n}{m} \text { 。(王枫供题) }
$$
用 $f(n)$ 表示正整数 $n$ 的二进制表示中数码 " 1 " 占所有数码的比例, 例如 $21=(10101)_2$, 则 $f(21)=\frac{3}{5}$.
(1)是否存在由 21 个不超过 2024 的正整数构成的非常值等差数列 $a_1, a_2, \cdots, a_{21}$, 使得 $f\left(a_1\right)=f\left(a_2\right)=\cdots=f\left(a_{21}\right)$ ? 证明你的结论;
(2)是否存在无穷多个正整数 $m$ ,使得 $f\left(m^2\right)>\frac{7}{10}$ ?证明你的结论.(何忆捷供题)