单选题 (共 14 题 ),每题只有一个选项正确
$\sin 600^{\circ}$ 的值是
$\text{A.}$ $\frac{1}{2}$
$\text{B.}$ $-\frac{1}{2}$
$\text{C.}$ $\frac{\sqrt{3}}{2}$
$\text{D.}$ $-\frac{\sqrt{3}}{2}$
函数 $y={a}^{|{x}|}({a}>1)$ 的图象是
$\text{A.}$ 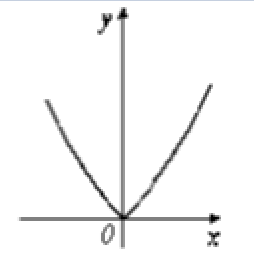 $\text{B.}$
$\text{B.}$ 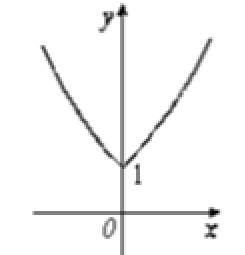 $\text{C.}$
$\text{C.}$ 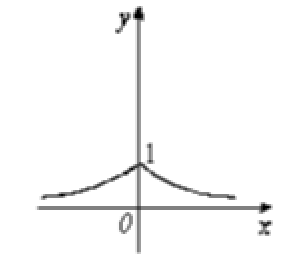 $\text{D.}$
$\text{D.}$ 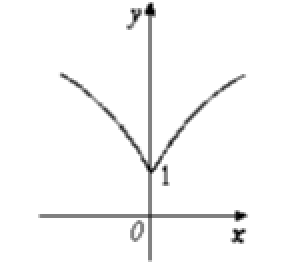
曲线的极坐标方程 $\rho=4 \sin \theta$ 化成直角坐标方程为
$\text{A.}$ $x^2+(y+2)^2=4$
$\text{B.}$ $x^2+(y-2)^2=4$
$\text{C.}$ $(x-2)^2+y^2=4$
$\text{D.}$ $(x+2)^2+y^2=4$
两条直线 $A_1 x+B_1 y+C_1=0, A_2 x+B_2 y+C_2=0$ 垂直的充要条件是
$\text{A.}$ $A_1 A_2+B_1 B_2=0$
$\text{B.}$ ${A}_1 {A}_2-{B}_1 {B}_2=0$
$\text{C.}$ $\frac{{A}_1 {~A}_2}{{B}_1 {B}_2}=-1$
$\text{D.}$ $\frac{{A}_1 {A}_2}{{~B}_1 {B}_2}=1$
函数 $f(x)=\frac{1}{x}(x \neq 0)$ 的反函数 $f^{-1}(x)=$
$\text{A.}$ $x(x \neq 0)$
$\text{B.}$ $\frac{1}{x}(x \neq 0)$
$\text{C.}$ $-x(x \neq 0)$
$\text{D.}$ $-\frac{1}{x}(x \neq 0)$
已知点 $P(\sin \alpha-\cos \alpha, \operatorname{tg} \alpha)$ 在第一象限, 则在 $(0,2 \pi)$ 内 $\alpha$ 的取值范围是
$\text{A.}$ $\left(\frac{\pi}{2}, \frac{3 \pi}{4}\right) \cup\left(\pi, \frac{5 \pi}{4}\right)$
$\text{B.}$ $\left(\frac{\pi}{4}, \frac{\pi}{2}\right) \cup\left(\pi, \frac{5 \pi}{4}\right)$
$\text{C.}$ $\left(\frac{\pi}{2}, \frac{3 \pi}{4}\right) \cup\left(\frac{5 \pi}{4}, \frac{3 \pi}{2}\right)$
$\text{D.}$ $\left(\frac{\pi}{4}, \frac{\pi}{2}\right) \cup\left(\frac{3 \pi}{4}, \pi\right)$
已知圆锥的全面积是底面积的 3 倍, 那么该圆锥的侧面展开图扇形的圆心角为
$\text{A.}$ $120^{\circ}$
$\text{B.}$ $150^{\circ}$
$\text{C.}$ $180^{\circ}$
$\text{D.}$ $240^{\circ}$
复数 $-i$ 的一个立方根是 $i$, 它的另外两个立方根是
$\text{A.}$ $\frac{\sqrt{3}}{2} \pm \frac{1}{2} i$
$\text{B.}$ $-\frac{\sqrt{3}}{2} \pm \frac{1}{2} i$
$\text{C.}$ $\pm \frac{\sqrt{3}}{2}+\frac{1}{2} i$
$\text{D.}$ $\pm \frac{\sqrt{3}}{2}-\frac{1}{2} i$
如果棱台的两底面积分别是 $S, S^{\prime}$, 中截面的面积是 $S_0$, 那么
$\text{A.}$ $2 \sqrt{2}=\sqrt{S}+\sqrt{S^{\prime}}$
$\text{B.}$ $S_0=\sqrt{S^{\prime} S}$
$\text{C.}$ $2 S_0=S+S^{\prime}$
$\text{D.}$ $S_0^2=2 S^{\prime} S$
3名医生和6名护士被分配到3所学校为学生体检, 每校分配 1 名医生和 2 名护士, 不同的分配方法共有
$\text{A.}$ 90 种
$\text{B.}$ 180 种
$\text{C.}$ 270 种
$\text{D.}$ 540 种
椭圆 $\frac{x^2}{12}+\frac{y^2}{3}=1$ 的焦点为 $\mathrm{F}_1$ 和 $\mathrm{F}_2$, 点 $P$ 在椭圆上, 如果线段 $P F_1$ 的中点在 $y$ 轴上, 那么 $\left|\mathrm{PF}_1\right|$ 是 $\left|\mathrm{PF}_2\right|$ 的
$\text{A.}$ 7 倍
$\text{B.}$ 5 倍
$\text{C.}$ 4 倍
$\text{D.}$ 3 倍
球面上有 3 个点, 其中任意两点的球面距离都等于大圆周长的 $1 / 6$, 经过这 3 个点的小圆的周长为 $4 \pi$, 那么这个球的半径为
$\text{A.}$ $4 \sqrt{3}$
$\text{B.}$ $2 \sqrt{3}$
$\text{C.}$ 2
$\text{D.}$ $\sqrt{3}$
在等比数列 $\left\{{a}_n\right\}$ 中, ${a}_1>1$, 且前 $n$ 项和 $S_n$ 满足 $\lim _{n \rightarrow \infty} S_n=\frac{1}{a_1}$, 那么 ${a}_1$ 的取值范围是
$\text{A.}$ $(1,+\infty)$
$\text{B.}$ $(1,4)$
$\text{C.}$ $(1,2)$
$\text{D.}$ $(1, \sqrt{2})$
填空题 (共 4 题 ),请把答案直接填写在答题纸上
设圆过双曲线 $\frac{x^2}{9}+\frac{y^2}{16}=1$ 的一个顶点和一个焦点, 圆心在此双曲线上, 则圆心到双曲线中心的距离是
$(x+2)^{10}\left(x^2-1\right)$ 的展开式中 ${x}^{10}$ 的系数为 $\qquad$ (用数字作答)。
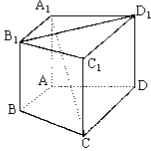
如图, 在直四棱柱 $A_1 B_1 C_1 D_1 A B C D$ 中, 当底面四边形 $A B C D$ 满足条件 $\qquad$时, 有 $A_1 C \perp B_1 D_1$ 。 (注:填上你认为正确的一种条件即可,不必考虑所有可能的情形。)
关于函数 $f(x)=4 \sin \left(2 x+\frac{\pi}{3}\right)(x \in R)$ ,有下列命题:
(1) 由 $f\left(x_1\right)=f\left(x_2\right)=0$ 可得 $x_1-x_2$ 必是 $\pi$ 的整数倍;
(2) $y=f(x)$ 的表达式可改写为 $y=4 \cos \left(2 x-\frac{\pi}{6}\right)$ ;
(3) $y=f(x)$ 的图象关于点 $\left(-\frac{\pi}{6}, 0\right)$ 对称;
(4) $y=f(x)$ 的图象关于直线 $x=-\frac{\pi}{6}$ 对称。
其中正确的命题的序号是_。(注: 把你认为正确的命题的序号都填上。)
解答题 (共 6 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
在 $\triangle \mathrm{ABC}$ 中, $a, b, c$ 分别是角 $A, B, a$ 的对边, 设 $a+c=2 b, A-C=\frac{\pi}{3}$ ,求$\sin B$
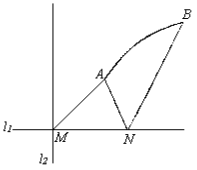
如图, 直线 $l_1$ 和 $l_2$ 相交于点 $M, l_1 \perp l_2$, 点 $N \in l_1$ 。以 $A, B$ 为端点的曲线段 $C$ 上的任一点到 $l_2$的距离与到点 $N$ 的距离相等, 若 $\triangle \mathrm{AMN}$ 为锐角三角形, $|\mathrm{AM}|=\sqrt{17},|\mathrm{AN}|=3$ 且 $|\mathrm{BN}|=6$ 。建立适当的坐标系, 求曲线段 $C$ 的方程。
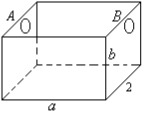
如图, 为处理含有某种杂质的污水, 要制造一底宽为 2 米的无盖长方体沉淀箱, 污水从 $A$ 孔流入, 经沉淀后从 $B$ 孔流出。设箱体的长度为 $a$ 米, 高度为 $b$ 米。已知流出的水中该杂质的质量分数与 $a, b$ 的乘积 $a b$ 成反比。现有制箱材料 60 平方米。问当 $a, b$ 各为多少米时, 经沉淀后流出的水中该杂质的质量分数最小 ( $A 、 B$ 孔的面积忽略不计)。
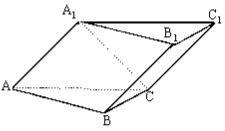
已知斜三棱柱 $A B C A_1 B_1 C_1$ 的侧面 $A_1 A C C_1$ 与底面 $A B C$ 垂直, $\angle \mathrm{ABC}=90^{\circ}, B C=2, A C=2 \sqrt{3}$, 且 $\mathrm{AA}_1 \perp \mathrm{A}_1 \mathrm{C}, \mathrm{AA}_1=\mathrm{A}_1 \mathrm{C} 。$
(I) 求侧棱 $\mathrm{A}_1 \mathrm{~A}$ 与底面 $A B C$ 所成角的大小;
(II) 求侧面 $A_1 A B B_1$ 与底面 $A B C$ 所成二面角的大小;
(III) 求顶点 $C$ 到侧面 $A_1 A B B_1$ 的距离。
设曲线 $C$ 的方程是 ${y}={x}^3-{x}$, 将 $C$ 沿 x 轴、 $y$ 轴正向分别平行移动 t s 单位长度后得曲线 $C_1$ 。
( I ) 写出曲线 $C_1$ 的方程;
(II) 证明曲线 $C$ 与 $C_1$ 关于点 $A\left(\frac{t}{2}, \frac{s}{2}\right)$ 对称;
(III) 如果曲线 $C$ 与 $C_1$ 有且仅有一个公共点, 证明 $s=\frac{t^3}{4}-t$ 且 ${t} \neq 0$ 。
已知数列 $\left\{{b}_{{n}}\right\}$ 是等差数列, ${b}_1=1, {~b}_1+{b}_2+\cdots+{b}_{10}=145$ 。
(I) 求数列 $\left\{b_n\right\}$ 的通项 $b_n$;
(II) 设数列 $\left\{b_n\right\}$ 的通项 $a_n=\log _a\left(1+\frac{1}{b_n}\right)$(其中 $a>0$, 且 $a \neq 1$ ),记 $S_n$ 是数列 $\left\{a_n\right\}$ 的前 n 项和。试比较 ${S}_{{n}}$ 与 $\frac{1}{3} \log _a b_{n+1}$ 的大小, 并证明你的结论。