一、解答题 (共 6 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
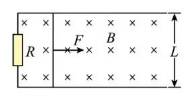
1. 如图所示, 两根足够长的光滑平行金属导轨固定于同一水平面内, 导轨电阻不计, 其间距为
。左端通过导线连接一个
的定值电阻, 整个导轨处在磁感应强度大小
, 方向坚直向下的匀强磁场中, 质量
、 电阻
长度为
的匀质金属杆垂直导轨放置, 且与导轨接触良好。在杆的中点施加一个垂直杆的水平拉力
, 使杆由静止开始运动, 拉力
的功率
保持不变, 当杆的速度
时撤去拉力
。求:
(1) 杆的速度为
时, 杆的加速度的大小;
(2) 从撤去拉力
到杆停下整个过程中, 杆上产生的热量
;
(3) 从撤去拉力
到杆停下整个过程中, 杆滑动的位移大小
。
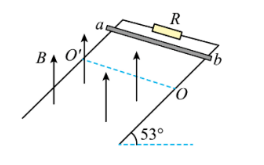
2. 如图所示, 电阻 不计且间距
的光滑平行金属导轨所在平面与水平面成
角, 上端接一阻值
的电阻, 虚线
下方有磁感应强度
方 向坚直向上的匀强磁场, 现将质量
、电阻
的金属杆
从斜面上由静止释放, 释放位置与虚线
之问的距离为
。金 属杆在下落的过程中与导轨一直垂直, 且保持良好接触, 导轨足 够长,
取
。求:
(1)金属杆
刚进有界磁场时的加速度;
(2)金属杆
在磁场中运动的最大速度大小;
(3)若金属杆
从进入磁场到达到最大速度经历的时间为
, 则这段时间内金属杆向下滑行的距离为多少?
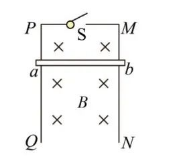
3. 如图所示,
和
是两根互相平行、间距为
、坚直放置的光滑金属导轨, 且处于磁 感应强度为
的匀强磁场中, 已知导轨足够长, 且电阻不计。
是一根不但与导轨垂直而且始终与导轨接触良好的金属杆, 金属 杆的质量为
, 电阻为
。将开关
闭合, 让
由静止开始自由 下落高度
后杆的速度达到最大。已知重力加速度为
。
(1)请大致再出金属杆的速度随时间变化的图像;
(2)金属杆在下落过程中通过金属杆的电量、产生的热量;
(3)金属枺下落这段高度需要的时间。
4. 如图所示, 电阻为
、半径为
的单匝圆形导体线圈两端与导轨
、 相连, 处于坚直向下磁场中, 其磁感应强度
随时间
变化规律为:
,
其中
、 为已知量。
、、 是三根材质和粗细相同的匀质金属棒,
的长度为
、电阻为
、质量为
。导轨
与
平行且间距为
, 导轨
与
平行且间距为
和
的长度相同且与
、 的夹角均为
。区域I和区域II是两个相邻的边长均为
的正方形 区域, 区域I中存在坚直向下、磁感应强度大小为
的匀强磁场。
时间内, 水平外力使棒
在区域I中某位置保持静止, 且其两 端分别与导轨
与
对齐。其余导体电阻均不计, 导轨均固定于 水平面内, 不计一切摩擦。
(1)
和
内, 分别比较棒
两端的电势高低, 并分 别求使棒
保持静止的水平外力
大小;
(2) 在
以后的某时刻, 撤去右侧圆形磁场, 若区域 I内的磁场 在外力作用下全部从区域I以速度
匀速运动到区域II时, 导体棒
速度恰好达到
且恰好进入区域II, 该过程棒
产生的焦耳热 为
, 求金属棒
与区域
左边界的初始距离
和该过程维持磁场 匀速运动的外力做的功
;
(3) 在 (2) 前提下, 若磁场运动到区域I时立刻停下, 求导体棒
运动到
时的速度
。

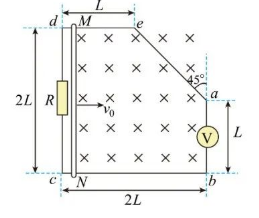
5. 光滑金属框架
置于水平面内,
, 各边长度如图所示。
边接入阻值为
的定值电 阻,
边接入理想电压表
, 导棒
平行于
, 不计框架与导 棒的电阻。匀强磁场垂直于框架平面, 磁感应强度大小为
。在 外力作用下,
沿框架以初始速度
从靠近
的位置向右运动, 导棒始终与
垂直且接触良好。
运动到
之前的过程中, 电 压表的示数恒为
。
(1) 试从功和能量转化关系的角度证明:
在
之问运动的 过程中, 切割磁感线产生的电动势
;
(2) 若定义“只类加速度”为通过单位位移内的速度改变量, 用公 式表示为
。请分析说明:
向右运动的整个过程中,
是 如何变化的?
(3)
由
向右运动到
的过程中, 安培力对导棒所做的功
为多少?
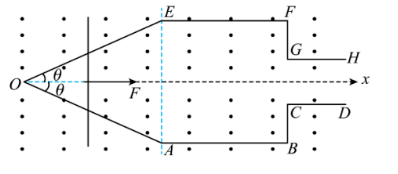
6. 如图所示, 匀强磁场垂直 于纸面向外且范围足够大, 磁感应强度的大小为
, 水平面 上固定不计电阻的关于
对称的足够长的轨道
和
。其中
且间距为
且间距为
,
、 与
轴的夹角均为
, 且
。一根粗细均匀的导体 棒长度为
、质量为
、单位长度的电阻为
, 用沿着
轴正方向向右的拉力
作用在导体棒的中点, 使其从
点开始 沿着
轴做匀速直线运动, 速度的大小为
。
木撤去 拉力, 同时断开
和
的连接, 且同时在
和
导轨的左 端上放一根质量为
、长度
的导体棒, 金属棒与导轨接触良好, 不计一切摩擦。求:
(1) 导体棒在
轨道上:时, 电流强度的大小;
(2)导体棒在
轨道上运动过程中, 产生的焦耳热;
(3)
和
都足够长,
末之后两棒产生的总焦耳热。