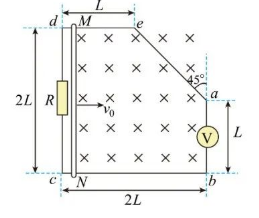
光滑金属框架 $a b c d e$ 置于水平面内, $\angle b=\angle c=\angle d=90^{\circ}$, 各边长度如图所示。 $c d$ 边接入阻值为 $R$ 的定值电 阻, $a b$ 边接入理想电压表 $\mathrm{V}$, 导棒 $M N$ 平行于 $c d$, 不计框架与导 棒的电阻。匀强磁场垂直于框架平面, 磁感应强度大小为 $B$ 。在 外力作用下, $M N$ 沿框架以初始速度 $v_0$ 从靠近 $c d$ 的位置向右运动, 导棒始终与 $b c$ 垂直且接触良好。 $M N$ 运动到 $a b$ 之前的过程中, 电 压表的示数恒为 $U$ 。
(1) 试从功和能量转化关系的角度证明: $M N$ 在 $d, e$ 之问运动的 过程中, 切割磁感线产生的电动势 $E=2 B L V_0$;
(2) 若定义“只类加速度”为通过单位位移内的速度改变量, 用公 式表示为 $A=\frac{\Delta v}{\Delta s}$ 。请分析说明: $M N$ 向右运动的整个过程中, $A$ 是 如何变化的?
(3) $M N$ 由 $c d$ 向右运动到 $a b$ 的过程中, 安培力对导棒所做的功 $W_A$ 为多少?