如图所示, 匀强磁场垂直 于纸面向外且范围足够大, 磁感应强度的大小为
(1) 导体棒在
(2)导体棒在
(3)
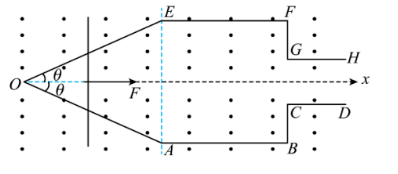
(1) 导体棒在
(2)导体棒在
(3)
