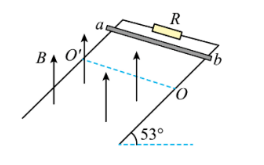
如图所示, 电阻 不计且间距 $L=\operatorname{lm}$ 的光滑平行金属导轨所在平面与水平面成 $53^{\circ}$ 角, 上端接一阻值 $R=3.5 \Omega$ 的电阻, 虚线 $O O^{\prime}$ 下方有磁感应强度 $B=1 \mathrm{~T}$ 方 向坚直向上的匀强磁场, 现将质量 $m=20 \mathrm{~g}$ 、电阻 $r=1 \Omega$ 的金属杆 $a b$ 从斜面上由静止释放, 释放位置与虚线 $O O^{\prime}$ 之问的距离为 $9 \mathrm{~cm}$ 。金 属杆在下落的过程中与导轨一直垂直, 且保持良好接触, 导轨足 够长, $g$ 取 $10 \mathrm{~m} / \mathrm{s}^2, \sin 53^{\circ}=0.8$ 。求:
（1）金属杆 $a b$ 刚进有界磁场时的加速度;
（2）金属杆 $a b$ 在磁场中运动的最大速度大小;
（3）若金属杆 $a b$ 从进入磁场到达到最大速度经历的时间为 $0.3 \mathrm{~s}$, 则这段时间内金属杆向下滑行的距离为多少?