单选题 (共 6 题 ),每题只有一个选项正确
使分式 $\frac{x}{2 x-4}$ 有意义的 $x$ 的取值范围是
$\text{A.}$ $x=2$
$\text{B.}$ $x \neq 2$
$\text{C.}$ $x=-2$
$\text{D.}$ $x \neq 0$
小马虎在下面的计算中只做对了一道题, 他做对的题目是.
$\text{A.}$ $(a+b)^2=a^2+b^2$
$\text{B.}$ $2 \times 10^{-4} \times 1 \times 10^3=2$
$\text{C.}$ $a^3+a^2=2 a^5$
$\text{D.}$ $\left(-2 a^3\right)^2=4 a^6$
下列说法正确的是
$\text{A.}$ $\frac{x+5}{3}$ 是单项式
$\text{B.}$ $\frac{1}{x}$ 是单项式
$\text{C.}$ $-2 a$ 是一次单项式
$\text{D.}$ $\frac{x y}{3}$ 的次数是 1 次
下列等式中,从左到右的变形是因式分解的是.
$\text{A.}$ $x^2+3 x-5=x(x+3)-5$
$\text{B.}$ $(x+5)^2=x^2+10 x+25$
$\text{C.}$ $(x+3)(x-2)=x^2+x-6$
$\text{D.}$ $x^2-5 x+6=(x-2)(x-3)$
图形经过平移、旋转或翻折运动后所具有的共同性质是
$\text{A.}$ 形状不变, 大小可能改变
$\text{B.}$ 大小不变, 形状可能改变
$\text{C.}$ 形状和大小都不变
$\text{D.}$ 形状和大小都可能改变
如图, 五角星绕着它的旋转中心旋转, 使得 $\triangle A B C$ 与 $\triangle D E F$ 重合,那么旋转角的度数至少为.
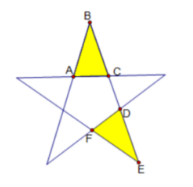
$\text{A.}$ $60^{\circ}$
$\text{B.}$ $120^{\circ}$
$\text{C.}$ $72^{\circ}$
$\text{D.}$ $144^{\circ}$
填空题 (共 12 题 ),请把答案直接填写在答题纸上
计算: $2^2 \times 2^4=$ (结果用幂的形式衣示).
将代数式 $5 x^{-3} y^2$ 化为只含有正整数指数幂的形式是
如果 $x^2+6 x+c$ 是一个完全平方式, 那么 $c=$
计算: $\frac{1}{x y-x} \cdot \frac{x}{y-1}=$
计算: $x^2 y\left(x^{-1}-y^{-1}\right)=$
小丽、小明练习打字, 小丽比小明每分钟多打 25 个字, 小丽打 300 个字的时间与小明 打 200 个字的时间相同. 如果设小明每分钟打 $x$ 个字, 那么根据题意可列方程是
已知线段 $A B$ 的长为 6 里米, 将它向左平移 2 厘米, 点 $A$ 平移到 $A^{\prime}$, 点 $B$ 平移到 $B^{\prime}$, 得 到线段 $A^{\prime} B^{\prime}$, 那么线段 $B B^{\prime}=$ 厘米.
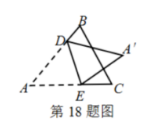
如图所示, 把 $\triangle A B C$ 沿直线 $D E$ 翻折后得到 $\triangle A^{\prime} D E$, 如果 $\angle A^{\prime} E C=36^{\circ}$, 那么 $\angle A^{\prime} E D=$ 度.
解答题 (共 9 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
计算: $\left(2 a b^3\right)^2 \cdot a+3 a^4 b^6 \div a$
计算: $\frac{a^2}{a-1}-a-1$
因式分解: $a^2-b^2+2 a^2 b-2 a b^2$
因式分解: $\left(a^2+a\right)^2-8\left(a^2+a\right)+12$
解方程: $\frac{4 x-1}{x-3}=2+\frac{1}{x-3}$
先化简, 再求值: $\frac{x^2-1}{x+2} \div\left(\frac{1}{x+2}-1\right)$, 其中 $x=\frac{4}{3}$ 。
小明骑自行车比步行每小时多 走 8 千米, 如果他步行 12 千米所用的时间与骑自行车 36 千米所用的时间相等, 求他骑自行车的速度。
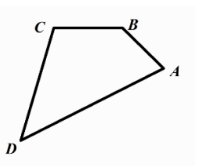
已知四边形 $A B C D$, 如果点 $D 、 C$ 关于直线 $M N$ 对称,
(1) 画出直线 $M N$;
(2) 画出四边形 $A B C D$ 关于直线 $M N$ 的对称图形。
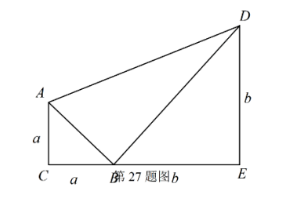
如图, 已知等腰直角三角形 $A C B$ 的边 $A C=B C=a$, 等腰直角三角形 $B E D$ 的边 $B E=D E=b$,
且 $a < b$, 点 $C 、 B 、 E$ 放置在一条直线上, 联结 $A D$ 。
(1) 求三角形 $A B D$ 的面积。
(2) 如果点 $P$ 是线段 $C E$ 的中点, 联结 $A P 、 D P$ 得到三角形 $A P D$, 求三角形 $A P D$ 的面 积。
(3)(2)中的三角形 $A P D$ 与二角形 $A B D$ 面积哪个较大? 大多少?
(结果都可用 $a 、 b$ 代数式表示, 并化简.)