科数网
题号:4016 题型:解答题 来源:上海市奉贤区七校联考2022学年第一学期七年级数学期末试卷
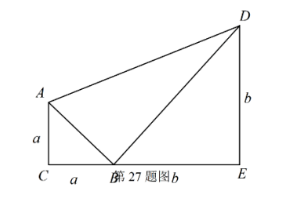
如图, 已知等腰直角三角形
A
C
B
的边
A
C
=
B
C
=
a
, 等腰直角三角形
B
E
D
的边
B
E
=
D
E
=
b
,
且
a
<
b
, 点
、
、
C
、
B
、
E
放置在一条直线上, 联结
A
D
。
(1) 求三角形
A
B
D
的面积。
(2) 如果点
P
是线段
C
E
的中点, 联结
、
A
P
、
D
P
得到三角形
A
P
D
, 求三角形
A
P
D
的面 积。
（3）（2）中的三角形
A
P
D
与二角形
A
B
D
面积哪个较大? 大多少?
(结果都可用
、
a
、
b
代数式表示, 并化简.)
A.
B.
C.
D.
0 人点赞
103 次查看
白板
加入试卷
答案：
解析：
答案与解析：
答案仅限会员可见
微信内自动登录
或
手机登录
或
微信扫码注册登录
点击我要
开通VIP