单选题 (共 10 题 ),每题只有一个选项正确
现实世界中,对称现象无处不在,中国的方块字中有些也具有对称性.下列美术字是轴对称图形的是
$\text{A.}$  $\text{B.}$
$\text{B.}$  $\text{C.}$
$\text{C.}$  $\text{D.}$
$\text{D.}$ 
掷两个质地均匀的小正方体,小正方体的六个面上分别标有 1 到 6 的数字.下列事件是必然事件的是
$\text{A.}$ 向上两面的数字和为 5
$\text{B.}$ 向上两面的数字和大于 1
$\text{C.}$ 向上两面的数字和大于 12
$\text{D.}$ 向上两面的数字和为偶数
2025年"五一"期间,全国旅游市场火爆.据文化和旅游部数据中心统计,国内旅游消费超过 1800 亿元( 1 亿 $=10^8$ )同比增长 $8 \%$ .将数据 1800 亿用科学记数法表示是
$\text{A.}$ $0.18 \times 10^{12}$
$\text{B.}$ $1.8 \times 10^{11}$
$\text{C.}$ $18 \times 10^{10}$
$\text{D.}$ $1.8 \times 10^{12}$
下列计算正确的是( )
$\text{A.}$ $a^2+a^3=a^5$
$\text{B.}$ $a^2 \cdot a^3=a^6$
$\text{C.}$ $\left(-a^3\right)^2=a^6$
$\text{D.}$ $a^8 \div a^2=a^4$
"漏壶"是中国古代一种全天候计时仪器,在它内部盛一定量的水,水从壶下的小孔漏出,壶内壁有刻度,人们根据壶中水面的位置计算时间.壶中水面高度 $y$(单位: cm )随漏水时间 $t$(单位:$h$ )的变化规律如图所示(不考虑水量变化对压力的影响)。水面高度从 48 cm 变化到 42 cm 所用的时间是
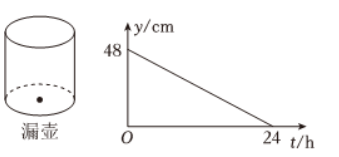
$\text{A.}$ $3 h$
$\text{B.}$ $4 h$
$\text{C.}$ $6 h$
$\text{D.}$ 12 h
某商场开展购物抽奖促销活动,抽奖盒中装有三个小球,它们分别标有 10 元、 20 元、 30 元,一次性随机摸出两个小球,摸出的两球上金额的和为 50 元的概率是( )
$\text{A.}$ $\frac{1}{6}$
$\text{B.}$ $\frac{1}{4}$
$\text{C.}$ $\frac{1}{3}$
$\text{D.}$ $\frac{1}{2}$
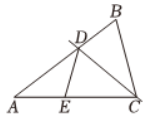
如图,在 $\triangle A B C$ 中,$A B=A C, D$ 是边 $A B$ 上的点,将 $\triangle B C D$ 沿直线 $C D$ 折叠,点 $B$ 的对应点 $E$ 恰好落在边 $A C$ 上.若 $\angle A=34^{\circ}$ ,则 $\angle A D E$ 的大小是( )
$\text{A.}$ $35^{\circ}$
$\text{B.}$ $37^{\circ}$
$\text{C.}$ $39^{\circ}$
$\text{D.}$ $41^{\circ}$
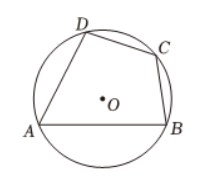
如图,四边形 $A B C D$ 内接于 $\odot O, \widehat{A B}=2 \widehat{C D}$ .若 $A B=6, C D=\sqrt{13}$ ,则 $\odot O$ 的半径是
$\text{A.}$ $\frac{13}{4}$
$\text{B.}$ $\frac{7}{2}$
$\text{C.}$ $\frac{9}{2}$
$\text{D.}$ 5
如图1,在 $\triangle A B C$ 中,$D$ 是边 $A C$ 上的定点.点 $P$ 从点 $A$ 出发,依次沿 $A B, B C$ 两边匀速运动,运动到点 $C$ 时停止.设点 $P$运动的路程为 $x, D P$ 的长为 $y, y$ 关于 $x$ 的函数图象如图2所示,其中 $M, N$ 分别是两段曲线的最低点。点 $N$ 的纵坐标是()
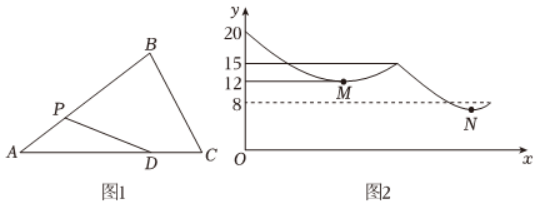
$\text{A.}$ $\frac{116}{17}$
$\text{B.}$ $\frac{120}{17}$
$\text{C.}$ $\frac{112}{15}$
$\text{D.}$ $\frac{116}{15}$
填空题 (共 6 题 ),请把答案直接填写在答题纸上
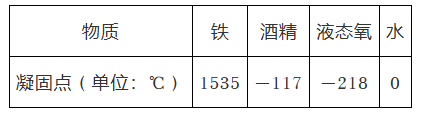
在标准大气压下,四种物质的凝固点如表所示,其中凝固点最低的物质是 $\qquad$ .
在平面直角坐标系中,某反比例函数 $y=\frac{k}{x}$ 的图象分别位于第一、第三象限.写出一个满足条件的 $k$ 的值是
方程 $\frac{1}{x-1}=\frac{4}{x^2-1}$ 的解是
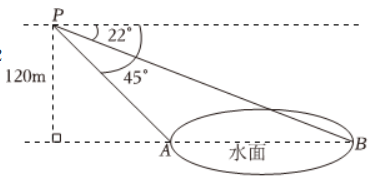
某科技小组用无人机测量一池塘水面两端 $A, B$ 的距离,具体过程如下:如图,将无人机垂直上升至距水面 120 m 的 $P$ 处,测得 $A$ 处的俯角为 $45^{\circ}, B$ 处的俯角为 2 $2^{\circ}$ ,则 $A, B$ 之间的距离是 $\qquad$ m.( $\tan 22^{\circ}$ 取 0.4$)$
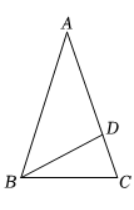
如图,在 $\triangle A B C$ 中,$A B=A C=10, B C=2 \sqrt{10}$ ,点 $D$ 在边 $A C$ 上,$C D=3$ .若点 $E$ 在边 $A B$ 上,满足 $C E$ $=B D$ ,则 $A E$ 的长是
已知二次函数 $y=a x^2+(a-2) x-2$( $a$ 为常数,且 $a \neq 0$ ).下列五个结论:
(1)该函数图象经过点 $(-1,0)$ ;
(2)若 $a=-1$ ,则当 $x>-1$ 时,$y$ 随 $x$ 的增大而减小;
(3)该函数图象与 $x$ 轴有两个不同的公共点;
(4)若 $a>2$ ,则关于 $x$ 的方程 $a x^2+(a-2) x-2=0$ 有一个根大于 0 且小于 1 ;
(5)若 $a>2$ ,则关于 $x$ 的方程 $\left|a x^2+(a-2) x-2\right|=2$ 的正数根只有一个.
其中正确的是 $\qquad$ ( 填写序号 )。
解答题 (共 8 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
解不等式组 $\left\{\begin{array}{ll}3 x-5 \leq 1 & \text {(1)} \\ 2 x+1>x & \text {(2)}\end{array}\right.$
如图,四边形 $A B C D$ 的对角线交于点 $O, A D \| B C$ .若﹎ㅡ,则 $A D=C B$ .
从(1)$O A=O C$ ,(2)$\angle A B C=\angle C D A$ ,(3)$A B=C D$ 这三个选项中选择一个作为条件,使结论成立,并说明理由。
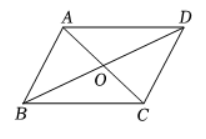
某校开展"中国诗词"竞赛,学生成绩为正整数,满分为5分。为了解本次竞赛的情况,从该校随机抽取 $m$ 名学生的成绩作为样本,将收集的数据整理并绘制成如下两幅不完整的统计图。
根据以上信息,解答下列问题:
(1)$m$ 的值是 $\qquad$ ,扇形统计图中" 5 分"对应的扇形的圆心角大小是 $\qquad$ .
(2)该校共有 1000 名学生参加竞赛,估计成绩超过 3 分的学生人数。
(3)从样本的众数、中位数中选择一个统计量,写出它的值并说明它的实际意义.
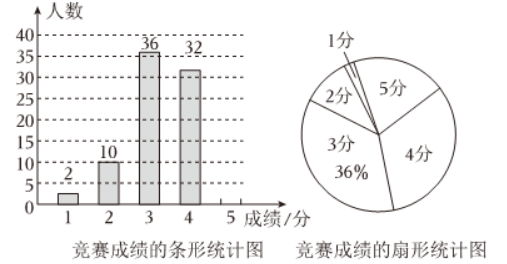
如图,点 $A, B, C, D$ 在 $\odot O$ 上,$B D$ 是直径,$\angle B A C=45^{\circ}$ ,过点 $C$ 作 $C E \| B D$ 交 $A B$ 的延长线于点
$E$ .
(1)求证:$C E$ 是 $\odot O$ 的切线.
(2)若 $B D=4, \tan \angle A B D=2$ ,求图中阴影部分的面积.
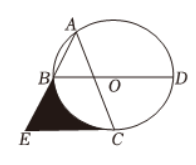
如图是由小正方形组成的 $3 \times 4$ 网格,每个小正方形的顶点叫作格点,矩形 $A B C D$ 的四个顶点都是格点.仅用无刻度直尺在给定网格中完成如下两个问题,每个问题的画线不得超过五条。
(1)如图1,$E$ 是格点,先将点 $E$ 绕点 $A$ 逆时针旋转 $90^{\circ}$ ,画对应点 $F$ ,再画直线 $F G$ 交 $A B$ 于点 $G$ ,使直线 $F G$ 平分矩形 $A B C D$ 的面积.
(2)如图2,先画点 $C$ 关于直线 $B D$ 的对称点 $M$ ,再画射线 $M N$ 交 $B D$ 于点 $N$ ,使 $M N \| A D$ .
某校数学小组开展以"羽毛球飞行路线"为主题的综合实践活动.研究背景 羽毛球飞行路线所在的平面与球网垂直.
收集数据 某次羽毛球飞行的高度 $y$(单位:$m$ )与距发球点的水平距离 $x$(单位:$m$ )的对应值如表(不考虑空气阻力)。
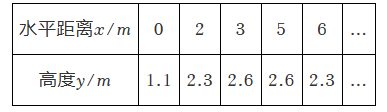
探索发现 数学小组借助计算机画图软件,建立平面直角坐标系、描点、连线(如图),发现羽毛球飞行路线是抛物线 $y=a x^2+b x$ +1.1 的一部分.
建立模型 求 $y$ 与 $x$ 的函数解析式(不要求写自变量取值范围)。
(1)羽毛球在此次飞行过程中,飞行的高度能否达到 2.8 m ?请说明理由.
(2)保持羽毛球飞行路线对应的抛物线的形状不变,改变发球方式,使其解析式变为 $y=a x^2+k x+1.1$ ,发球点与球网的水平距离是 5 m .若羽毛球飞过球网正上方时,飞行的高度超过 2.1 m ,且球的落地点与球网的水平距离小于 6 m .求 $k$ 的取值范围.
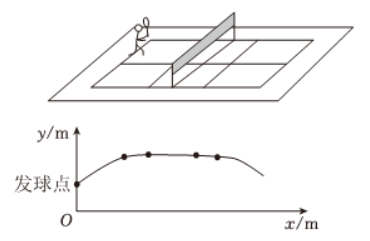
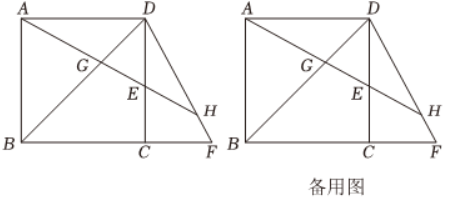
如图,四边形 $A B C D$ 是正方形,点 $E$ 在边 $C D$ 上,点 $F$ 在边 $B C$ 的延长线上,$D E=C F$ ,射线 $A E$ 交对角线 $B D$ 于点 $G$ ,交线段 $D F$ 于点 $H$ .
(1)求证:$D H=G H$ .
(2)求证:$A G \cdot E H=E G \cdot G H$ .
(3)若 $\frac{G E}{E H}=n$ ,直接写出 $\frac{D H}{D F}$ 的值(用含 $n$ 的式子表示).
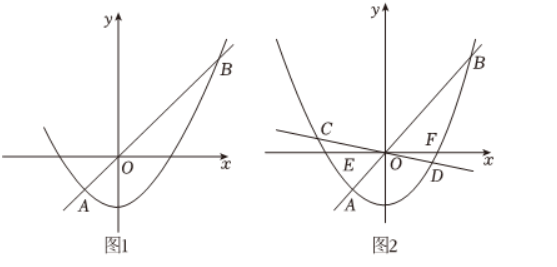
抛物线 $y=\frac{1}{4} x^2-3$ 与直线 $y=x$ 交于 $A, B$ 两点( $A$ 在 $B$ 的左边).
(1)求 $A, B$ 两点的坐标.
(2)如图1,若 $P$ 是直线 $A B$ 下方抛物线上的点,过点 $P$ 作 $x$ 轴的平行线交抛物线于点 $M$ ,过点 $P$ 作 $y$ 轴的平行线交线段 $A B$ 于点 $N$ ,满足 $P M=P N$ ,求点 $P$ 的横坐标.
(3)如图2,经过原点 $O$ 的直线 $C D$ 交抛物线于 $C, D$ 两点(点 $C$ 在第二象限),连接 $A C, B D$ 分别交 $x$ 轴于 $E, F$ 两点.若 $S_{\triangle D O F}=$ $\frac{3}{4} S_{\triangle C O E}$ ,求直线 $C D$ 的解析式.