单选题 (共 8 题 ),每题只有一个选项正确
已知命题"$p: \exists x \in(-3,+\infty), x^2 \leqslant 9$",则 $\neg p$ 是
$\text{A.}$ $\forall x \in(-3,+\infty), x^2>9$
$\text{B.}$ $\forall x \in(-3,+\infty), x^2 \leqslant 9$
$\text{C.}$ $\exists x \in(-3,+\infty), x^2 \geqslant 9$
$\text{D.}$ $\exists x \in(-3,+\infty), x^2>9$
已知集合 $A=\{-1,0,1,2\}, B=\{x \in \mathbf{N} \mid x < 3\}$ ,那么集合 $A \cup B$ 等于
$\text{A.}$ $[-1,3)$
$\text{B.}$ $\{0,1,2\}$
$\text{C.}$ $\{-1,0,1,2\}$
$\text{D.}$ $\{-1,0,1,2,3\}$
不等式 $\frac{7}{2 x-1}>1$ 的解集为
$\text{A.}$ $\left\{x \left\lvert\, \frac{1}{2} < x < 4\right.\right\}$
$\text{B.}$ $\left\{x \left\lvert\, \frac{1}{4} < x < 2\right.\right\}$
$\text{C.}$ $\left\{x \left\lvert\, x < \frac{1}{2}\right.\right.$ 或 $\left.x>4\right\}$
$\text{D.}$ $\left\{x \left\lvert\, x < \frac{1}{4}\right.\right.$ 或 $\left.x>2\right\}$
设函数 $f(x)=\left\{\begin{array}{l}x^2+1, x \leqslant 1, \\ \frac{2}{x}, x>1,\end{array}\right.$ 则 $f(f(3))$ 等于
$\text{A.}$ $\frac{1}{5}$
$\text{B.}$ 3
$\text{C.}$ $\frac{2}{3}$
$\text{D.}$ $\frac{13}{9}$
已知函数 $f(x)$ 的定义域为 $(0,5)$ ,则函数 $g(x)=f(x-1)+\frac{1}{\sqrt{x-2}}$ 的定义域为
$\text{A.}$ $[2,4)$
$\text{B.}$ $[2,6)$
$\text{C.}$ $(2,4)$
$\text{D.}$ $(2,6)$
定义集合 $A$ 和 $B$ 的运算:$A \bigcirc B=\{(x, y) \mid x \in A, y \in B\}$ ,若集合 $A=\{1,2,3\}, B=\{2,3\}$ ,则 $A \cup B$ 的真子集个数为
$\text{A.}$ 31
$\text{B.}$ 32
$\text{C.}$ 62
$\text{D.}$ 63
已知定义在 $\mathbf{R}$ 上的偶函数 $f(x)$ 在 $(0,+\infty)$ 上单调,且 $f(-\sqrt{2})>f(\sqrt{3})$ ,则 $f(-3), f(\sqrt{5})$ , $f(\pi)$ 的大小顺序是
$\text{A.}$ $f(\sqrt{5}) < f(-3) < f(\pi)$
$\text{B.}$ $f(\pi) < f(-3) < f(\sqrt{5})$
$\text{C.}$ $f(-3) < f(\sqrt{5}) < f(\pi)$
$\text{D.}$ $f(\sqrt{5}) < f(\pi) < f(-3)$
已知命题 $p$ :存在 $a \in \mathbf{R}$ 且 $a \neq 0$ ,对于任意的 $x \in \mathbf{R}$ ,使得 $f(x+a) < f(x)+f(a) ; q_1: f(x)$ 在 $\mathbf{R}$上单调递减,且 $f(x)>0$ 恒成立;$q_2: f(x)$ 在 $\mathbf{R}$ 上单调递增,且存在 $x_0 < 0$ 使得 $f\left(x_0\right)=0$ .下列说法正确的是
$\text{A.}$ 只有 $q_1$ 是 $p$ 的充分条件
$\text{B.}$ 只有 $q_2$ 是 $p$ 的充分条件
$\text{C.}$ $q_1, q_2$ 都是 $p$ 的充分条件
$\text{D.}$ $q_1, q_2$ 都不是 $p$ 的充分条件
多选题 (共 3 题 ),每题有多个选项正确
若 $a, b, c \in \mathbf{R}$ ,则下列命题正确的是
$\text{A.}$ 若 $a c^2>b c^2$ ,则 $a>b$
$\text{B.}$ 若 $a>b$ 且 $\frac{1}{a}>\frac{1}{b}$ ,则 $a b < 0$
$\text{C.}$ 若 $b>a>0$ ,则 $a^3+a < b^3+b$
$\text{D.}$ 若 $a>b>0$ 且 $c < 0$ ,则 $a+c < b+c$
已知函数 $f(x)$ 的定义域为 $[1,+\infty)$ ,且 $f(\sqrt{x}+1)=2 \sqrt{x}+x$ ,则
$\text{A.}$ $f(x)=x^2-1(x \geqslant 1)$
$\text{B.}$ $f(x)$ 的值域为 $[-1,+\infty)$
$\text{C.}$ $f(x)$ 在 $[1,+\infty)$ 上单调递增
$\text{D.}$ $f\left(\frac{1}{x}\right)$ 的值域为 $[0,+\infty)$
已知函数 $f(x)$ 的定义域为 $\mathbf{R}, \forall x, y \in \mathbf{R}, f(x+y)=f(x) f(y)$ ,且 $f(1)=\frac{1}{2}$ ,则
$\text{A.}$ $f(2)=\frac{1}{4}$
$\text{B.}$ 函数 $f(x)$ 在 $\mathbf{R}$ 上单调递增
$\text{C.}$ $f(x+1) < f(x)$
$\text{D.}$ $f(x+2)-f(x+1) < f(x+1)-f(x)$
填空题 (共 3 题 ),请把答案直接填写在答题纸上
已知幂函数 $y=x^\alpha$ 的图象经过点 $(2, \sqrt{2})$ 和点 $(16, n)$ ,则 $n=$
已知两正数 $x, y$ ,满足 $x+\frac{2}{y}=1$ ,则 $\frac{2}{x}+y$ 的最小值为
定义域为 $\mathbf{R}$ 的偶函数 $g(x)$ 在 $[0,+\infty)$ 上单调递减,且 $g(1)=0$ ,若关于 $x$ 的不等式( $a x +1) g(x-1) \geqslant(b x-2) g(1-x)$ 的解集为 $[0,+\infty)$ ,则 $b^2+a$ 的最小值为
解答题 (共 5 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
(1)已知 $f(x)=3 x+2$ ,求 $f(2 x+5)$ 的解析式;
(2)已知 $f(x)$ 为二次函数,且 $f(x+1)+f(x-1)=2 x^2-4 x$ ,求 $f(x)$ 的解析式.
已知命题 $p: \forall x \in \mathbf{R}$ ,不等式 $2 t x^2+2 t x+1>0$ 恒成立,当命题 $p$ 为真命题时,实数 $t$ 的取值集合为 $A$ 。
(1)求集合 $A$ ;
(2)设非空集合 $B=\{t \mid a-2 < t+1 < 2 a\}$ ,若"$x \in A$"是"$x \in B$"的充分不必要条件,求实数 $a$ 的取值范围.
已知函数 $f(x)=x^2-3(a+1) x+2 a^2+3 a(a \in \mathbf{R})$ .
(1)当 $a=1$ 时,求函数 $f(x)$ 的最小值;
(2)若关于 $x$ 的不等式 $f(x) < 0$ 的解集为 $(1,5)$ ,求实数 $a$ 的值;
(3)设关于 $x$ 的不等式 $f(x) < 0$ 的解集为 $A, B=[-1,1]$ ,若 $A \cap B=\varnothing$ ,求实数 $a$ 的取值范围.
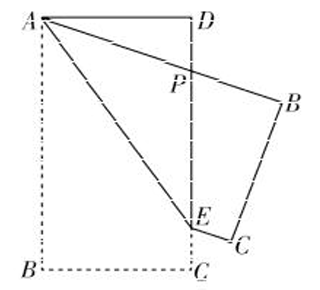
已知矩形 $A B C D$ 的周长为 20 ,其中 $A B>A D$ ,如图所示,$E$ 为 $C D$ 边上一动点,把四边形 $A B C E$ 沿 $A E$ 折叠,使得 $A B$ 与 $D C$ 交于点 $P$ .设 $D P=x, P E=y$ .
(1)若 $A D=3$ ,将 $y$ 表示成 $x$ 的函数 $y=f(x)$ ,并求定义域;
(2)在(1)条件下,判断并证明 $y=f(x)$ 的单调性;
(3)求 $\triangle A D P$ 面积的最大值.
已知函数 $f(x)$ 的定义域为 $\mathbf{R}$ ,给定集合 $D$ ,若 $f(x)$ 满足对任意 $x_1, x_2 \in \mathbf{R}$ ,存在实数 $\lambda$ ,当 $x_1-x_2 \in D$ 时,都有 $\lambda\left[f\left(x_1\right)-f\left(x_2\right)\right] \in D$ ,则称 $f(x)$ 是 $D$ 上的"$\lambda$ 级优函数".
(1)请写出一个 $\{1\}$ 上的" 1 级优函数",并说明理由.
(2)已知 $f(x)$ 是 $[2,3]$ 上的" 2 级优函数",
(i)证明:$f(x+6)-f(x)=3$ ;
(ii )当 $x \in[0,1]$ 时,$f(x)=a x+\frac{b}{x+1}$ ,其中 $a, b \in \mathbf{Z}$ ,求 $a, b$ 的值.