单选题 (共 8 题 ),每题只有一个选项正确
已知复数 $z$ 满足 $\frac{\sqrt{3}- i }{z}=1+\sqrt{3} i$, 则 $|z|=$
$\text{A.}$ 2
$\text{B.}$ 1
$\text{C.}$ $\sqrt{2}$
$\text{D.}$ $\sqrt{3}$
已知集合 $A=\{x \in Z | | x-1 \mid < 3\}, B=\{x \mid 0 \leq x \leq 3\}$, 则 $A \cap B=(\quad)$
$\text{A.}$ $\{0,1,2,3\}$
$\text{B.}$ $\{-1,0,1,2\}$
$\text{C.}$ $\{x \mid 0 \leq x \leq 3\}$
$\text{D.}$ $\{x \mid-2 < x < 4\}$
" $2^a>1, \quad \log _2 b>1$ "是" $2^{a+b}>4$ "的(
$\text{A.}$ 充分不必要条件
$\text{B.}$ 必要不充分条件
$\text{C.}$ 充要条件
$\text{D.}$ 既不充分也不必要条件
已知单位向量 $\vec{a}, \vec{b}$ 满足 $|\vec{a}+\vec{b}|=1$, 则下列说法正确的是 ()
$\text{A.}$ $\langle\vec{a}, \vec{b}\rangle=150^{\circ}$
$\text{B.}$ $|\vec{a}-\vec{b}|=3$
$\text{C.}$ 向量 $\vec{a}+\vec{b}$ 在向量 $\vec{a}$ 上的投影向量为 $\frac{\sqrt{3}}{2} \vec{a}$
$\text{D.}$ $\vec{b} \perp\left(\vec{a}+\frac{1}{2} \vec{b}\right)$
函数 $f(x)=\cos 2 x-\cos x$ 是 ( )
$\text{A.}$ 偶函数, 且最小值为 -2
$\text{B.}$ 偶函数, 且最大值为 2
$\text{C.}$ 周期函数, 且在 $\left(0, \frac{\pi}{2}\right)$ 上单调递增
$\text{D.}$ 非周期函数, 且在 $\left(\frac{\pi}{2}, \pi\right)$ 上单调递减
印度数学家卡普列加在一次旅行中, 遇到猛烈的暴风雨, 他看到路边写有 3025 的一块牌子被䢃成了两半,一半上写着 30 , 另一半上写着 25 , 这时, 他发现 $30+25=55,55^2=3025$, 即将劈成两半的数加起来, 再平方,正好是原来的数字。数学家将 3025 等符合上述规律的数字称之为雷劈数(或卡普列加数)。则在下列数组:92,81,52,40,21,14中随机选择两个数,其中恰有一个数是雷劈数的概率是()
$\text{A.}$ $\frac{8}{15}$
$\text{B.}$ $\frac{3}{5}$
$\text{C.}$ $\frac{1}{3}$
$\text{D.}$ 0
已知函数 $f(x)=\left\{\begin{array}{l}-a x+1, x < a \\ (x-1)^2, x \geq a\end{array}\right.$ 的值域为 R , 则实数 $a$ 的取值范围是 ( )
$\text{A.}$ $(-\infty, 0)$
$\text{B.}$ $(-\infty,-1]$
$\text{C.}$ $[-1,1]$
$\text{D.}$ $[-1,0)$
记正项数列 $\left\{a_n\right\}$ 的前 $n$ 项积为 $T_n$, 已知 $\left(a_n-1\right) T_n=2 a_n$, 若 $a_n < \frac{1001}{1000}$, 则 $n$ 的最小值是 ( )
$\text{A.}$ 999
$\text{B.}$ 1000
$\text{C.}$ 1001
$\text{D.}$ 1002
多选题 (共 3 题 ),每题有多个选项正确
现有甲、乙两组数据, 甲组数据为: $x_1, x_2, \cdots, x_{16}$; 乙组数据为: $3 x_1-9,3 x_2-9, \cdots, 3 x_{16}-9$, 若甲组数据的平均数为 $m$, 标准差为 $n$, 极差为 $a$, 第 60 百分位数为 $b$, 则下列说法一定正确的是 ( )
$\text{A.}$ 乙组数据的平均数为 $3 m-9$
$\text{B.}$ 乙组数据的极差为 $3 a$
$\text{C.}$ 乙组数据的第 60 百分位数为 $3 b-9$
$\text{D.}$ 乙组数据的标准差为 $n$
在三棱台 $A B C-A_1 B_1 C_1$ 中, 侧面 $A C C_1 A_1$ 是等腰梯形且与底面垂直, $A_1 C_1=1, A A_1=\sqrt{2}$, $A C=B C=3, A B=3 \sqrt{2}$, 则下列说法正确的是()
$\text{A.}$ $A_1 A \perp B C$
$\text{B.}$ $V_{A-A B C}=9 V_{B-A, B C_1}$
$\text{C.}$ $V_{A_1-A B C}=2 V_{B-A_1 C C_1}$
$\text{D.}$ 三棱台 $A B C-A_1 B_1 C_1$ 的体积为 $\frac{13}{6}$
已知函数 $f(x)$ 及其导函数 $f^{\prime}(x)$ 的定义域均为 R , 记 $g(x)=f^{\prime}(x)$, 若 $f(x)+f(2-x)=2$, $g(x-1)$ 为偶函数,则下列说法一定正确的是()
$\text{A.}$ $f(0)+f(1)+f(2)=3$
$\text{B.}$ $g(x+4)=g(x)$
$\text{C.}$ $f(x+4)=f(x)$
$\text{D.}$ $g\left(\frac{1}{2}\right)=g\left(\frac{3}{2}\right)$
填空题 (共 3 题 ),请把答案直接填写在答题纸上
若 $3 \cos \alpha+4 \sin \alpha=5$, 则 $\tan \alpha=$
已知椭圆 $C: \frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$ 的左、右焦点分别为 $F_1 、 F_2$, 过 $F_2$ 且垂直于 $x$ 轴的直线交椭圆于 $A 、 B$ 两点, 若 $\triangle A F_1 B$ 为等边三角形, 则椭圆 $C$ 的离心率为
现有甲、乙、丙等 7 位同学, 各自写了一封信, 然后都投到同一个邮箱里.若甲、乙、丙 3 位同学分别从邮箱里随机抽取一封信, 则这 3 位同学抽到的都不是自己写的信的不同取法种数是 $\qquad$ (用数字作答)。
解答题 (共 5 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
在 $\triangle A B C$ 中, 内角 $A , B, C$ 所对的边分别为 $a, b, c$, 且 $\sin B \cdot \sin C=\sin A, a=2$.
(1) 求 $\triangle A B C$ 的面积 S ;
(2) 若 $b^2+c^2=12$, 求 A .
如图, 四棱锥 $P-A B C D$ 的底面是正方形, 且 $A B=2, P A \perp P B$. 四棱锥 $P-A B C D$ 的体积为 $\frac{4}{3}$.
(1) 证明: 平面 $P A B \perp$ 平面 $A B C D$;
(2) 求平面 $P A B$ 与平面 $P C D$ 夹角的余弦值.
已知函数 $f(x)= e ^{2 x}-2(a+1) e ^x+2 a x+2 a+1(a>0)$.
(1) 求函数 $f(x)$ 在 $x=0$ 处的切线方程;
(2) 讨论函数 $f(x)$ 的单调性;
(3) 若函数 $f(x)$ 存在两个零点 $x_1, x_2$, 且 $x_1+x_2>0$, 求实数 $a$ 的取值范围.
密室逃脱是当下非常流行的解压放松游戏, 现有含甲在内的 7 名成员参加密室逃脱游戏, 其中 3 名资深玩家, 4 名新手玩家, 甲为新手玩家.
(1)在某个游戏环节中, 需随机选择两名玩家进行对抗, 若是同级的玩家对抗, 双方获胜的概率均为$\frac{1}{2}$; 若是资深玩家与新手玩家对抗, 新手玩家获胜的概率为 $\frac{1}{3}$, 求在该游戏环节中, 获胜者为甲的概率;
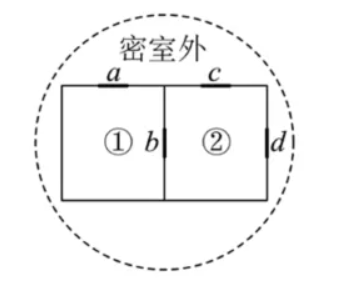
(2)甲作为上一轮的获胜者参加新一轮游戏:如图,有两间相连的密室,设两间密室的编号分别为(1)和 (2).密室(1)有 2 个门, 密室(2)有 3 个门(每个门都可以双向开),甲在每个密室随机选择 1 个门出去,若走出密室则挑战成功. 若甲的初始位置为密室(1), 设其挑战成功所出的密室号为 $X(X=1,2)$, 求 $X$ 的分布列.
已知数列 $\left\{a_n\right\}$ 的前 $n$ 项和为 $S_n$, 且 $S_n=2 a_n+n-3$.
(1) 求数列 $\left\{a_n\right\}$ 的通项公式;
(2) 设 $b_n=\left\{\begin{array}{l}k, n=a_k-1 \\ b_{n-1}+2 k, a_k-1 < n < a_{k+1}-1\end{array}, k \in N^*\right.$
(i) 当 $k \geq 2, n=a_{k+1}-1$ 时, 求证: $b_{n-1} \geq\left(a_k-1\right) \cdot b_n$;
(ii) 求 $\sum_{i=1}^{S_n-n} b_i$.