一、单选题 (共 15 题,每小题 5 分,共 50 分,每题只有一个选项正确)
设 $f(x)$ 有二阶连续导数, 且 $f^{\prime}(0)=0, \lim _{x \rightarrow 0} \frac{f^{\prime \prime}(x)}{|x|}=1$, 则( )
$\text{A.}$ $f(0)$ 是 $f(x)$ 的极大值.
$\text{B.}$ $f(0)$ 是 $f(x)$ 的极小值.
$\text{C.}$ $(0, f(0))$ 是曲线 $y=f(x)$ 的拐点.
$\text{D.}$ $f(0)$ 不是 $f(x)$ 的极值, $(0, f(0))$ 也不是曲线 $y=f(x)$ 的拐点.
设 $f^{\prime}\left(x_0\right)=f^{\prime \prime}\left(x_0\right)=0, f^{\prime \prime \prime}\left(x_0\right)>0$ 则下列选项正确的是
$\text{A.}$ $f^{\prime}\left(x_0\right)$ 是 $f^{\prime}(x)$ 的极大值
$\text{B.}$ $f\left(x_0\right)$ 是 $f(x)$ 的极大值
$\text{C.}$ $f\left(x_0\right)$ 是 $f(x)$ 的极小值
$\text{D.}$ $\left(x_0, f\left(x_0\right)\right)$ 是曲线 $y=f(x)$ 的拐点
已知函数 $y=f(x)$ 对一切 $x$ 满足$x f^{\prime \prime}(x)+3 x\left[f^{\prime}(x)\right]^2=1-e^{-x} \text {. }$
若 $f^{\prime}\left(x_0\right)=0\left(x_0 \neq 0\right)$ ,则
$\text{A.}$ $f\left(x_0\right)$ 是 $f(x)$ 的极大值
$\text{B.}$ $f\left(x_0\right)$ 是 $f(x)$ 的极小值
$\text{C.}$ $\left(x_0, f\left(x_0\right)\right)$ 是曲线 $y=f(x)$ 的拐点
$\text{D.}$ $f\left(x_0\right)$ 不是 $f(x)$ 的极值, $\left(x_0, f\left(x_0\right)\right)$ 也不是曲线 $y=f(x)$ 的拐点
设函数 $f(x)$ 的导数在 $x=a$ 处连续,又 $\lim _{x \rightarrow a} \frac{f^{\prime}(x)}{x-a}=-1$ ,则
$\text{A.}$ $x=a$ 是 $f(x)$ 的极小值点.
$\text{B.}$ $x=a$ 是 $f(x)$ 的极大值点.
$\text{C.}$ (a, f(a))$ 是曲线 $y=f(x)$ 的拐点
$\text{D.}$ $x=a$ 不是 $f(x)$ 的极值点, $(a, f(a))$ 也不是曲线 $y=f(x)$ 的拐点
设函数 $f(x)$ 在 $(-\infty,+\infty)$ 内连续,其导函数的图形如下图所示,则 $f(x)$ 有

$\text{A.}$ 一个极小值点和两个极大值点
$\text{B.}$ 两个极小值点和一个极大值点
$\text{C.}$ 两个极小值点和两个极大值点
$\text{D.}$ 三个极小值点和一个极大值点
已知函数 $f(x, y)$ 在点 $(0,0)$ 的某个邻域内连续,且 $\lim _{\substack{x \rightarrow 0 \\ y \rightarrow 0}} \frac{f(x, y)-x y}{\left(x^2+y^2\right)^2}=1$ ,则
$\text{A.}$ 点 $(0,0)$ 不是 $f(x, y)$ 的极值点
$\text{B.}$ 点 $(0,0)$ 是 $f(x, y)$ 的极大值点
$\text{C.}$ 点 $(0,0)$ 是 $f(x, y)$ 的极小值点
$\text{D.}$ 根据所给条件无法判断点 $(0,0)$ 是否为 $f(x, y)$ 的极值点
设函数 $f(x)$ 在 $(-\infty,+\infty)$ 内连续,其导函数的图形如下图所示,则 $f(x)$ 有

$\text{A.}$ 一个极小值点和两个极大值点
$\text{B.}$ 两个极小值点和一个极大值点
$\text{C.}$ 两个极小值点和两个极大值点
$\text{D.}$ 三个极小值点和一个极大值点
设函数 $f(x)$ 连续,且 $f^{\prime}(0)>0$, 则存在 $\delta>0$ ,使得
$\text{A.}$ $f(x)$ 在 $(0, \delta)$ 内单调增加
$\text{B.}$ $f(x)$ 在 $(-\delta, 0)$ 内单调减少
$\text{C.}$ 对任意的 $x \in(0, \delta)$ 有 $f(x)>f(0)$
$\text{D.}$ 对任意的 $x \in(-\delta, 0)$ 有 $f(x)>f(0)$
设 $f(x)=|x(1-x)|$ ,则
$\text{A.}$ $x=0$ 是 $f(x)$ 的极值点,但 $(0,0)$ 不是曲线 $y=f(x)$ 的拐点
$\text{B.}$ $x=0$ 不是 $f(x)$ 的极值点,但 $(0,0)$ 是曲线 $y=f(x)$ 的拐点
$\text{C.}$ $x=0$ 是 $f(x)$ 的极值点,且 $(0,0)$ 是曲线 $y=f(x)$ 的拐点
$\text{D.}$ $x=0$ 不是 $f(x)$ 的极值点, $(0,0)$ 也不是曲线 $y=f(x)$的拐点
设 $f(x)=|x(1-x)|$. 则
$\text{A.}$ $x=0$ 是 $f(x)$ 的极值点,但 $(0,0)$ 不是曲线 $y=f(x)$ 的拐点
$\text{B.}$ $x=0$ 不是 $f(x)$ 的极值点,但 $(0,0)$ 是曲线 $y=f(x)$ 的拐点
$\text{C.}$ $x=0$ 是 $f(x)$ 的极值点,且 $(0,0)$ 是曲线 $y=f(x)$ 的拐点
$\text{D.}$ $x=0$ 不是 $f(x)$ 的极值点, $(0,0)$ 也不是曲线 $y=f(x)$的拐点
当 $a$ 取下列哪个值时,函数 $f(x)=2 x^3-9 x^2+12 x-a$恰好有两个不同的零点
$\text{A.}$ 2
$\text{B.}$ 4
$\text{C.}$ 6
$\text{D.}$ 8
设 $f(x)=x \sin x+\cos x$ , 下列命题中正确的是
$\text{A.}$ $f(0)$ 是极大值, $f\left(\frac{\pi}{2}\right)$ 是极小值
$\text{B.}$ $f(0)$ 是极小值, $f\left(\frac{\pi}{2}\right)$ 是极大值
$\text{C.}$ $f(0)$ 是极大值, $f\left(\frac{\pi}{2}\right)$ 也是极大值
$\text{D.}$ $f(0)$ 是极小值, $f\left(\frac{\pi}{2}\right)$ 也是极小值
设函数 $f(x)=\int_0^{x^2} \ln (2+t) \mathrm{d} t$ ,则 $f^{\prime}(x)$ 的零点个数为
$\text{A.}$ 0
$\text{B.}$ 1
$\text{C.}$ 2
$\text{D.}$ 3
设函数 $f(x)=x^2(x-1)(x-2)$ ,则 $f^{\prime}(x)$ 的零点个数为
$\text{A.}$ 0
$\text{B.}$ 1
$\text{C.}$ 2
$\text{D.}$ 3
二、填空题 (共 7 题, 每小题 5 分,共 20 分, 请把答案直接填写在答题纸上)
设 $\left\{\begin{array}{l}x=1+t^{2}, \\ y=\cos t,\end{array}\right.$ 则 $\frac{\mathrm{d}^{2} y}{\mathrm{~d} x^{2}}=$
函数 $y=y(x)$ 由方程 $\sin \left(x^2+y^2\right)+e^x-x y^2=0$ 所确定,则 $\frac{\mathrm{d} y}{\mathrm{~d} x}=$
设函数 $y=y(x)$ 由参数方程 $\left\{\begin{array}{l}x=t-\ln (1+t) \\ y=t^3+t^2\end{array}\right.$ 所确定,则 $\frac{\mathrm{d}^2 y}{\mathrm{~d} x^2}=$
设方程 $e^{x y}+y^2=\cos x$ 确定的 $y$ 为 $x$ 的函数,则 $\frac{\mathrm{d} y}{\mathrm{~d} x}=$
曲面 $z=x^2+y^2$ 与平面 $2 x+4 y-z=0$ 平行的切平面的方程是
曲线 $y=\ln x$ 上与直线 $x+y=1$ 垂直的切线方程为
曲线 $y=(x-5) x^{\frac{2}{3}}$ 的拐点坐标为
三、解答题 ( 共 18 题,满分 80 分,解答过程应写出必要的文字说明、证明过程或演算步骤 )
(1) 设 $f, g$ 为连续可微函数, $u=f(x, x y), v=g(x+x y)$, 求 $\frac{\partial u}{\partial x} \cdot \frac{\partial v}{\partial x}$.
(2) 设矩阵 ${A}$ 和 ${B}$ 满足关系式 ${A B}={A}+2 {B}$, 其中 ${A}=\left(\begin{array}{lll}3 & 0 & 1 \\ 1 & 1 & 0 \\ 0 & 1 & 4\end{array}\right)$, 求矩阵 ${B}$.
设 $\left\{\begin{array}{l}x=\cos \left(t^{2}\right), \\ y=t \cos \left(t^{2}\right)-\int_{1}^{t^{2}} \frac{1}{2 \sqrt{u}} \cos u \mathrm{~d} u,\end{array}\right.$ 求 $\frac{\mathrm{d} y}{\mathrm{~d} x}, \frac{\mathrm{d}^{2} y}{\mathrm{~d} x^{2}}$ 在 $t=\sqrt{\frac{\pi}{2}}$ 的值.
已知函数 $y=\frac{2 x^2}{(1-x)^2}$ ,试求其单调区间,极值点,图形的凹凸性,拐点和渐近线,并画出函数图形.
运用导数的知识作函数 $y=(x+6) e^{\frac{1}{x}}$ 的图形.
设 $y=\frac{x^3+4}{x^2}$.
(1)求函数的增减区间及极值;
(2)函数图像的凹凸区间及拐点;
(3)求其渐近线;
(4)作出其图形.
求函数 $f(x)=\int_0^{x^2}(2-t) e^{-t} \mathrm{~d} t$ 的最大值和最小值.
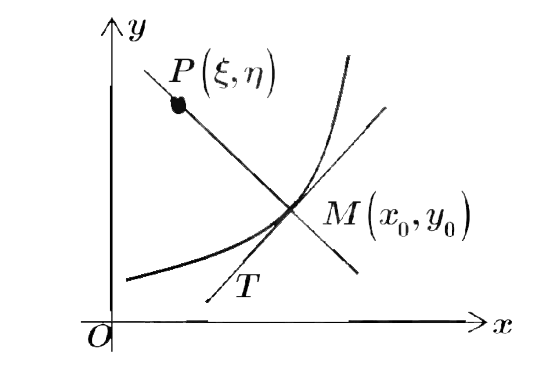
如图,设曲线 $L$ 的方程为 $y=f(x)$ ,且 $f^{\prime \prime}(x)>0$ ,又 $M T 、 M P$ 分别为该曲线在点 $M\left(x_0, y_0\right)$ 处的切线和法线,已知线段 $M P$ 的长度为 $\frac{\left[1+\left(y_0^{\prime}\right)^2\right]^{\frac{3}{2}}}{y_0^{\prime \prime}}$ (其中, $y_0^{\prime}=y^{\prime}\left(x_0\right)$, $\left.y_0^{\prime \prime}=y^{\prime \prime}\left(x_0\right)\right)$ ,试推导出点 $P(\xi, \eta)$ 的坐标表达式.
设函数 $y=y(x)$ 由方程 $2 y^3-2 y^2+2 x y-x^2=1$ 所确定,试求 $y=y(x)$ 的驻点,并判别它是否为极值点.
一商家销售某种商品的价格满足关系 $p=7-0.2 x$ (万元吨), $x$ 为销售量(单位: 吨),商品的成本函数是 $C=3 x+1$ (万元).
(1) 若销售一吨商品,政府要征税 $t$ (万元),求该商家获最大利润时的销售量;
(2) $t$ 为何值时,政府税收总额最大?
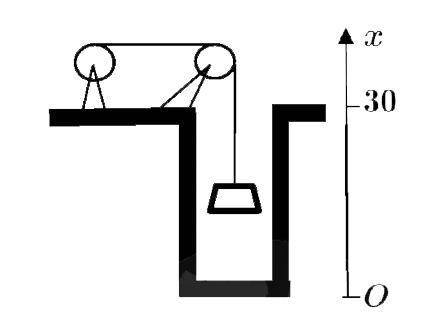
为清除井底的污泥,用缆绳将抓斗放人井底,抓起污泥后提出井口(见图),已知井深 $30 \mathrm{~m}$ ,抓斗自重 $400 \mathrm{~N}$ ,缆绳每米 $50 \mathrm{~N}$ ,抓斗抓起的污泥重 $2000 \mathrm{~N}$ ,提升速度为 $3 \mathrm{~m} / \mathrm{s}$ ,在提升的过程中,污泥以 $20 \mathrm{~N} / \mathrm{s}$ 的速率从缝隙中漏掉,现将抓起污泥的抓斗提升至井口,问克服重力需做多少焦耳的功?(说明:
(1) $1 \mathrm{~N} \times 1 \mathrm{~m}=1 \mathrm{~J} ; \mathrm{m}, \mathrm{N}, \mathrm{s}, \mathrm{J}$ 分别表示米,牛顿,秒,焦耳;
(2) 抓斗的高度位于井口上方的缆绳长度忽略不计).
已知函数 $y=\frac{x^3}{(x-1)^2}$ ,求:
(1)函数的增减区间及极值;
(2)函数图形的凹凸区间及拐点;
(3) 函数图形的渐进线.
求函数 $y=(x-1) e^{\frac{\pi}{2}+\arctan x}$ 的单调区间和极值,并求该函数图形的渐近线.
已知两曲线 $y=f(x)$ 与 $y=\int_0^{\arctan x} e^{-t^2} \mathrm{dt}$ 在点 $(0,0)$处的切线相同,写出此切线方程,并求极限 $\lim _{n \rightarrow \infty} n f\left(\frac{2}{n}\right)$.
设函数 $y=f(x)$ 由方程 $x y+2 \ln x=y^4$ 所确定,则曲线 $y=f(x)$ 在点 $(1,1)$ 处的切线方程是
设 $a>1, f(t)=a^t-a t$ 在 $(-\infty,+\infty)$ 内的驻点为 $t(a)$. 问 $a$ 为何值时, $t(a)$ 最小? 并求出最小值.
已知曲线 $L$ 的方程为 $\left\{\begin{array}{l}x=t^2+1 \\ y=4 t-t^2\end{array} \quad(t \geq 0)\right.$.
(1) 讨论 $L$ 的凹凸性;
(2) 过点 $(-1,0) $引$ L$ 的切线,求切点 $\left(x_0, y_0\right)$ ,并写出切线的方程;
(3) 求此切线与 $L$ (对应于 $x \leq x_0$ 的部分) 及 $x$ 轴所围成的平面图形的面积.
设函数 $y=y(x)$ 由方程 $y \ln y-x+y=0$ 确定,试判断曲线 $y=y(x)$ 在点 $(1,1)$ 附近的凹凸性.
设函数 $f(x)=\int_0^1|t(t-x)| \mathrm{d} t(0 < x < 1)$ ,求 $f(x)$ 的极值、单调区间以及曲线 $y=f(x)$ 的凹凸区间.