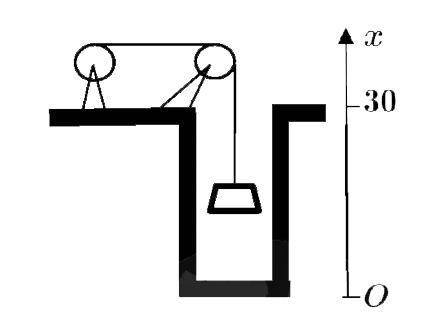
为清除井底的污泥,用缆绳将抓斗放人井底,抓起污泥后提出井口(见图),已知井深 $30 \mathrm{~m}$ ,抓斗自重 $400 \mathrm{~N}$ ,缆绳每米 $50 \mathrm{~N}$ ,抓斗抓起的污泥重 $2000 \mathrm{~N}$ ,提升速度为 $3 \mathrm{~m} / \mathrm{s}$ ,在提升的过程中,污泥以 $20 \mathrm{~N} / \mathrm{s}$ 的速率从缝隙中漏掉,现将抓起污泥的抓斗提升至井口,问克服重力需做多少焦耳的功?(说明:
(1) $1 \mathrm{~N} \times 1 \mathrm{~m}=1 \mathrm{~J} ; \mathrm{m}, \mathrm{N}, \mathrm{s}, \mathrm{J}$ 分别表示米,牛顿,秒,焦耳;
(2) 抓斗的高度位于井口上方的缆绳长度忽略不计).
(1) $1 \mathrm{~N} \times 1 \mathrm{~m}=1 \mathrm{~J} ; \mathrm{m}, \mathrm{N}, \mathrm{s}, \mathrm{J}$ 分别表示米,牛顿,秒,焦耳;
(2) 抓斗的高度位于井口上方的缆绳长度忽略不计).
