单选题 (共 12 题 ),每题只有一个选项正确
设集合 $A=\left\{x \mid x^{2}-1>0\right\}, B=\left\{x \mid \log _{2} x>0\right\}$, 则 $A \cap B=$ ( )
$\text{A.}$ $\{x \mid x > 1\}$
$\text{B.}$ $\{x \mid x > 0\}$
$\text{C.}$ $\{x \mid x < -1\}$
$\text{D.}$ $\{x \mid x < -1$ 或 $x > 1\}$
已知 $a, b \in R, i$ 是虚数单位. 若 $(1+i)(1-b i)=a$, 则 $\frac{a}{b}$ 的值为 ( )
$\text{A.}$ $3$
$\text{B.}$ $2$
$\text{C.}$ $-2$
$\text{D.}$ $-3$
下列说法中错误的是 ( )
$\text{A.}$ 命题 “ $\forall x > 1, x^{2}-x > 0$ ” 的否定是 “ $\exists x_{0} > 1, x_{0}^{2}-x_{0} \leq 0$ ”.
$\text{B.}$ 在 $\triangle A B C$ 中, $A < B \Leftrightarrow \sin A < \sin B \Leftrightarrow \cos A > \cos B$.
$\text{C.}$ 已知某 6 个数据的平均数为 3 , 方差为 2 , 现又加入一个新数据 3 , 则此时这 7 个数的平均数和方 差不变.
$\text{D.}$ 从装有完全相同的 4 个红球和 2 个黄球的盒子中任取 2 个小球, 则事件 “至多一个红球” 与 “都 是红球” 互斥且对立.
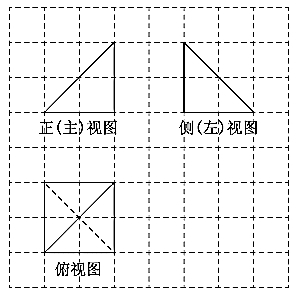
某三棱锥的三视图如图所示,已知网格纸上小正方形的边长为1,该三棱锥所有表面积中,最大面的面积为 ( )
$\text{A.}$ $2$
$\text{B.}$ $2\sqrt2$
$\text{C.}$ $2\sqrt3$
$\text{D.}$ $4\sqrt2$
已知平面向量 $\vec{a}=(\sqrt{3},-1),|\vec{b}|=\sqrt{2}$, 且 $(\vec{a}+2 \vec{b}) \cdot(\vec{a}-\vec{b})=2$, 则 $|\vec{a}-\vec{b}|=(\quad)$
$\text{A.}$ $\sqrt{2}$
$\text{B.}$ $2$
$\text{C.}$ $\sqrt{3}$
$\text{D.}$ $3$
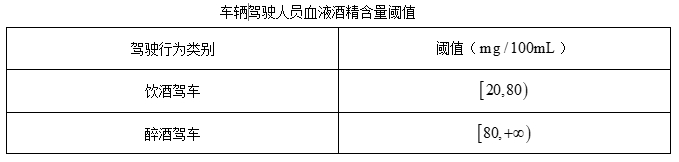
电影《流浪地球》中反复出现这样的人工语音: “道路干万条, 安全第一条, 行车不规范, 辛人两 行泪” 成为网络热句.讲的是 “开车不喝酒, 喝酒不开车” 2019 年, 公安部交通管理局下发《关于治理酒驾醉驾违法犯罪行为的指导意见》, 对综合治理酒驾醉驾违法犯罪行为提出了新规定, 根据国家质量监督检验检疫总局下发的标准, 车辆驾驶人员饮酒后或者醉酒后驾车血液中的酒精含量阈值见表.经过反复试验, 一般情况下, 某人喝一瓶筥酒后酒精在人体血液中的变化规律的“散点图”见图,
且图表所示的函数模型 $y=\left\{\begin{array}{l}40 \sin \left(\frac{\pi}{3} x\right)+13,0 \leq x < 2 \\ 90 \cdot e^{-0.5 x}+14, x \geq 2\end{array}\right.$, 假设该人喝一瓶㗭酒后至少经过
$n\left(n \in N^{*}\right)$ 小时才可以驾车,则 $n$ 的值为(参考数据: $\ln 15 \approx 2.71, \ln 30 \approx 3.40$ ) ( )

$\text{A.}$ $5$
$\text{B.}$ $6$
$\text{C.}$ $7$
$\text{D.}$ $8$
古希腊哲学家毕达哥拉斯曾说过:“美的线型和其他一切美的形体都必须有对称形式”.在中华传统文化里,建筑、器物、书法、诗歌、对联、绘画几乎无不讲究对称之美.如清代诗人黄柏权的《茶壶回文诗》(如图)以连环诗的形式展现,20个字绕着茶壶成一圆环,不论顺着读还是逆着读,皆成佳作.数学与生活也有许多奇妙的联系,如2020年02月02日(20200202)被称为世界完全对称日(公历纪年日期中数字左右完全对称的日期).数学上把20200202这样的对称数叫回文数,两位数的回文数共有9个(11,22,…,99),则共有多少个这样的三位回文数 ( )

$\text{A.}$ 64
$\text{B.}$ 72
$\text{C.}$ 80
$\text{D.}$ 90
设 $a=\log _{5} 4, b=\ln 2, c=\pi^{0.1}$, 则 ( )
$\text{A.}$ $a < b < c $
$\text{B.}$ $b < a < c$
$\text{C.}$ $ c < b < a$
$\text{D.}$ $a < c < b$
$f(x)=2 f(4-x)-x^{2}+2 x-1$, 则 $y=f(x)$ 在 $(2, f(2))$ 处的切线方程为 ( )
$\text{A.}$ $2 x-y-3=0$
$\text{B.}$ $2 x+3 y+7=0$
$\text{C.}$ $2 x-y+3=0$
$\text{D.}$ $2 x+3 y-7=0$
已知 $\triangle A B C$ 的内角 $A, B, C$ 对的边分别为 $a, b, c, \sin A+\sin B=\frac{3}{2} \sin C$ 当内角 $C$ 最 大且 $b=3$ 时, $\triangle A B C$ 的面积等于 ( )
$\text{A.}$ $\frac{9+3 \sqrt{3}}{4}$
$\text{B.}$ $2 \sqrt{3}$
$\text{C.}$ $2 \sqrt{5}$
$\text{D.}$ $\frac{3 \sqrt{6}-3 \sqrt{2}}{4}$
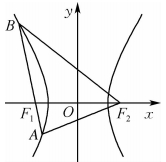
如图, 已知 $F_{1}, F_{2}$ 分别为双曲线 $C: \frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=1(a>0, b>0)$ 的左右焦点, 过 $F_{1}$ 的直线与双 曲线 $C$ 的左支交于 $A 、 B$ 两点, 连接 $A F_{2}, B F_{2}$, 在 $\triangle A B F_{2}$ 中, $A B=B F_{2}, \cos \angle A B F_{2}=\frac{31}{32}$, 则双曲线的离心率为 ( )
$\text{A.}$ $2$
$\text{B.}$ $\sqrt{2}$
$\text{C.}$ $\sqrt{3}$
$\text{D.}$ $\frac{3 \sqrt{2}}{2}$
已知函数 $f(x)=\cos \left(\omega x-\frac{2 \pi}{3}\right)(\omega>0), x_{1} 、 x_{2} 、 x_{3} \in[0, \pi]$, 且 $\forall x \in[0, \pi]$ 都有
$f\left(x_{1}\right) \leq f(x) \leq f\left(x_{2}\right)$, 满足 $f\left(x_{3}\right)=0$ 的实数 $x_{3}$ 有且只有 3 个, 给出下述四个结论:
(1)满足题目条件的实数 $x_{1}$ 有且只有 1 个;
(2)满足题目条件的实数 $x_{2}$ 有且只有 1 个;
(3) $f(x)$ 在 $\left(0, \frac{\pi}{10}\right)$ 上单调递增;
(4) $\omega$ 的取值范围是 $\left(\frac{13}{6}, \frac{19}{6}\right]$.
其中正确的个数是 ( )
$\text{A.}$ 1
$\text{B.}$ 2
$\text{C.}$ 3
$\text{D.}$ 4
填空题 (共 4 题 ),请把答案直接填写在答题纸上
若实数 $x, y$ 满足约束条件 $\left\{\begin{array}{l}x-3 y+4 \geq 0 \\ 3 x-y-4 \leq 0, \\ x+y \geq 0\end{array}\right.$. 则 $z=3 x+2 y$ 的最小值是
已知抛物线 $y^{2}=2 p x(p>0)$ 的焦点 $F$ 到准线的距离为 2 , 过焦点 $F$ 的直线与抛物线交于 $A, B$
两点, 且 $|A F|=3|F B|$, 则线段 $A B$ 的中点到 $y$ 轴的距离为
若二项式 $(x^{2}+\frac{a}{x})^{7} $ 的展开式的各项系数之和为$-1$, 则含 $ x^{-1 }$ 项的系数是
已知菱形 $A B C D$ 的边长为 4 , 对角线 $B D=4$, 将 $\triangle A B D$ 沿着 $B D$ 折叠, 使得二面角 $A-B D-C$为 $120^{\circ}$, 则三棱雉 $A-B C D$ 的外接球的表面积为
解答题 (共 7 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
已知数列 $\left\{a_{n}\right\}, S_{n}$ 是 $a_{n}$ 的前 $n$ 项的和, 且满足 $S_{n}=2 a_{n}-1\left(n \in N^{*}\right)$, 数列 $\left\{b_{n}\right\}$ 是等差数列, $b_{2}+b_{6}=a_{4}, a_{5}-b_{4}=2 b_{6} .$
(1) 求 $\left\{a_{n}\right\},\left\{b_{n}\right\}$ 的通项公式;
(2) 设数列 $\left\{S_{n}\right\}$ 的前 $n$ 项和为 $T_{n}$, 设 $
c_{n}=(-1)^{n} \frac{\left(T_{n}+b_{n+2}\right) b_{3 n+4}}{b_{n+1} b_{n+2}} $, 求 $c_{n}$ 的前 $n$ 项的和 $D_{n}$.
如图, 在三棱雉 $A-B C D$ 中, $\triangle A B C$ 是边长为 3 的等边三角形, $C D=C B, C D \perp$ 平面 $A B C$, 点 $M 、 N$ 分别为 $A C 、 C D$ 的中点, 点 $P$ 为线段 $B D$ 上一点, 且 $B M / /$ 平面 $A P N$.
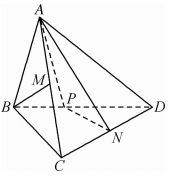
(1) 求证: $B M \perp A N$;
(2) 求平面 $A P N$ 与平面 $A B C$ 所成角的正弦值.
已知圆 $C:(x-1)^{2}+y^{2}=16$, 点 $F(-1,0), P$ 是圆 $C$ 上一动点, 若线段 $P F$ 的垂直平分线和 $C P$ 相交于点 $M$.
(1) 求点 $M$ 的轨迹方程 $E$.
(2) $A, B$ 是 $M$ 的轨迹方程与 $x$ 轴的交点 (点 $A$ 在点 $B$ 左边), 直线 $G H$ 过点 $T(4,0)$ 与轨迹 $E$ 交 于 $G, H$ 两点, 直线 $A G$ 与 $x=1$ 交于点 $N$, 求证: 动直线 $N H$ 过定点.
公元 1651 年, 法国一位著名的统计学家德梅赫 (Demere) 向另一位著名的数学家帕斯卡 (B. Pascal) 提出了一个问题, 帕斯卡和费马(Fermat)讨论了这个问题, 后来惠更斯 (C. Huygens) 也加入了讨 论, 这三位当时全欧洲乃至全世界最优秀的科学家都给出了正确的解答. 该问题如下: 设两名运动员 约定谁先赢 $k\left(k>1, k \in N^{*}\right)$ 局, 谁便赢得全部奖金 $a$ 元. 每局甲赢的概率为 $p(0 < p < 1)$, 乙赢的概 率为 $1-p$, 且每场比赛相互独立. 在甲赢了 $m(m < k)$ 局, 乙赢了 $n(n < k)$ 局时, 比赛意外终止.奖 金该怎么分才合理? 这三位数学家给出的答案是: 如果出现无人先赢 $k$ 局则比赛意外终止的情况, 甲、 乙便按照比赛再继续进行下去各自赢得全部奖金的概率之比 $P_{\text {甲 }}: P_{\text {乙 分配奖金. }}$
(1)规定如果出现无人先赢 $k$ 局则比赛意外终止的情况, 甲、乙便按照比赛再继续进行下去各自赢 得全部奖金的概率之比 $P_{\text {甲 }}: P_{乙}$ 分配奖金.若 $k=4, m=2, n=1, p=\frac{3}{4}$, 求 $P_{\text {甲 }}: P_{\text {乙 }}$.
(2) 记事件 $A$ 为 “比赛继续进行下去乙赢得全部奖金”, 试求当 $k=4, m=2, n=1$ 时比赛继续 进行下去甲赢得全部奖金的概率 $f(p)$, 并判断当 $p \geq \frac{4}{5}$ 时, 事件 $A$ 是否为小概率事件, 并说明理 由.规定: 若随机事件发生的概率小于 $0.05$, 则称该随机事件为小概率事件.
已知函数 $f(x)=e^{x}\left(x^{2}+m x+m^{2}\right), g(x)=a x^{2}+x+a x \ln x$.
(1) 若函数 $f(x)$ 在 $x=-1$ 处取极小值, 求实数 $m$ 的值;
(2) 设 $m=0$, 若对任意 $x \in(0,+\infty)$, 不等式 $f(x) \geq g(x)$ 恒成立, 求实数 $a$ 的值.
已知曲线 $C$ 的极坐标方程是 $\rho=4 \cos \theta$, 以极点为平面直角坐标系的原点, 极轴为 $x$ 轴的正半轴, 建立平面直角坐标系, 直线 $l$ 的参数方程是 $\left\{\begin{array}{l}x=m+\frac{\sqrt{2}}{2} t \\ y=\frac{\sqrt{2}}{2} t\end{array}\right.$ ( $t$ 为参数).
(1) 若直线 $l$ 与曲线 $C$ 相交于 $A 、 B$ 两点, 且 $|A B|=\sqrt{14}$, 试求实数 $m$ 的值;
(2)设 $M(x, y)$ 为曲线 $C$ 上任意一点, 求 $x+y$ 的取值范围.
已知函数 $f(x)=|2 x-1|-|x+1|$.
(1)求不等式 $f(x) < 2$ 的解集;
(2)若关于 $x$ 的不等式 $f(x) \leq a-\frac{a^{2}}{2}$ 有解,求 $a$ 的取值范围.