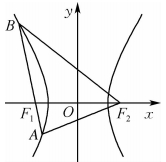
如图, 已知 $F_{1}, F_{2}$ 分别为双曲线 $C: \frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=1(a>0, b>0)$ 的左右焦点, 过 $F_{1}$ 的直线与双 曲线 $C$ 的左支交于 $A 、 B$ 两点, 连接 $A F_{2}, B F_{2}$, 在 $\triangle A B F_{2}$ 中, $A B=B F_{2}, \cos \angle A B F_{2}=\frac{31}{32}$, 则双曲线的离心率为 ( )
A
$2$
B
$\sqrt{2}$
C
$\sqrt{3}$
D
$\frac{3 \sqrt{2}}{2}$
E
F