解答题 (共 8 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
若实数 $\tau$ 满足: 对任意正整数 $x, y, z$, 均有 $x^2+2 y^2+4 z^2+8 \geq 2 x(y+z+\tau),$
则称 $\tau$ 为 "平生数". 记最大的平生数为 $\tau_0$.
(1) 求 $\tau_0$ 的值;
(2) 求方程 $x^2+2 y^2+4 z^2+8=2 x\left(y+z+\tau_0\right)$ 的所有正整数解 $(x, y, z)$.
(董秋仙供题)
设 $P$ 为平面凸多边形, 若线段 $A B$ 的两端点在 $P$ 的边界上, 并且过 $A, B$ 与 $A B$垂直的两条直线之间的区域(含边界)包含 $P$ ,则称线段 $A B$ 为 "锦弦". 求最大的正整数 $k$ ,使得任意平面凸多边形 $P$ 都有 $k$ 条锦弦。(王枫供题)
证明:任意正整数的平方均可表示为 $\frac{(a-b)^2+(b-c)^2+(c-a)^2}{2(a b+b c+c a)}$ 的形式,其中 $a, b, c$ 为正整数. (杨标桂供题)
在 $n \times n$ 的方格表中, 若两个方格有公共边, 则称它们是相邻的. 若 $l$ 个互异方格 $A_1, A_2, \cdots, A_l$ 满足 $A_i$ 和 $A_{i+1}$ 相邻 $(1 \leq i \leq l-1)$, 则称它们为一条长度为 $l$ 的 "龙". 求最大的正整数 $k$, 使得可以给每个方格填上 0 或者 1 , 并且对任意一个方格 $A$, 和以 $A$ 中数字为首项的 0,1 序列 $m_1, m_2, \cdots, m_k$, 都存在从 $A$ 开始的长度为 $k$的龙, 方格中数字依次是 $m_1, m_2, \cdots, m_k$. (欧阳泽轩供题)
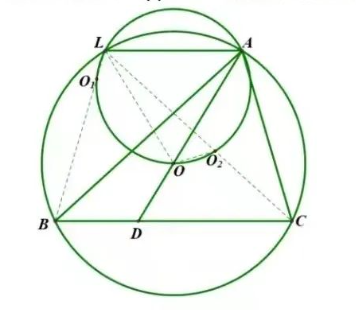
在锐角 $\triangle A B C$ 中, $A B>A C, O$ 为外心. 设 $D$ 为边 $B C$ 上一点, $O_1, O_2$ 分别为 $\triangle A B D$ 和 $\triangle A C D$ 的外心, $\triangle A O_1 O_2$ 的外接圆与 $\odot O$ 交于不同于点 $A$ 的点 $L$.
证明: $A, O, D$ 三点共线当且仅当 $A L / / B C$. (杨标桂供题)
求方程
$$
\frac{\sqrt{3}+2 \sin 2 x}{\sqrt{3}+2 \sin x}=\sqrt{3} \sin x+\frac{\cos 2 x}{2 \cos x}
$$
在 $\left(0, \frac{\pi}{2}\right)$ 内的解. (李胜宏供题)
设 $a$ 为正整数, $f_a(x)=x^4+a x^2+1$. 定义集合
$P_a=\left\{p \mid p\right.$ 为素数, 且存在正整数 $k$ 使得 $f_a(2 k)$ 是 $p$ 的倍数 $\}$ 。
(1) 证明: 对任意正整数 $a, P_a$ 为无限集;
(2) 若 $P_a$ 的任意两个元素之差是 8 的倍数, 求正整数 $a$ 的最小值. (杨晓鸣供题)
一项考试的可能得分为 $0,1,2, \cdots, 150$, 有 100 名考生 $P_1, P_2, \cdots, P_{100}$ 考完后依顺时针围成一圈交流成绩, 记 $P_i$ 的得分为 $a_i$. 每个考生 $P_i$ 比较自己与相邻两人 $P_{i-1}, P_{i+1}$ (下标按模 100 理解) 的得分, 定义 $P_i$ 的激励值 $f_i$ 为:
$$
\begin{aligned}
& \qquad f_i= \begin{cases}a_i\left(a_{i-1}+a_{i+1}-a_i\right), & a_i < \min \left\{a_{i-1}, a_{i+1}\right\}, \\
a_i\left(\max \left\{a_{i-1}, a_i, a_{i+1}\right\}-a_i\right), & a_i \geq \min \left\{a_{i-1}, a_{i+1}\right\} .\end{cases} \\
& \text { 记 } S=f_1+f_2+\cdots+f_{100} .
\end{aligned}
$$
(1) 求 $S$ 的最大值;
(2) 求使得 $f_1, f_2, \cdots, f_{100}$ 两两不等的 $S$ 的最大值. (何忆捷供题)