单选题 (共 7 题 ),每题只有一个选项正确
设函数 $f(x)=x \cdot \tan x \cdot e^{\sin x}$ ,则 $f(x)$ 是
$\text{A.}$ 偶函数
$\text{B.}$ 无界函数
$\text{C.}$ 周期函数
$\text{D.}$ 单调函数
设函数 $f(x)$ 对任意 $x$ 均满足等式 $f(1+x)=a f(x)$ ,且有 $f^{\prime}(0)=b$ ,其中 $a, b$ 为非零常数,则
$\text{A.}$ $f(x)$ 在 $x=1$ 处不可导
$\text{B.}$ $f(x)$ 在 $x=1$ 处可导,且 $f^{\prime}(1)=a$
$\text{C.}$ $f(x)$ 在 $x=1$ 处可导,且 $f^{\prime}(1)=b$
$\text{D.}$ $f(x)$ 在 $x=1$ 处可导,且 $f^{\prime}(1)=a b$
向量组 $\alpha_1, \alpha_2 \cdots, \alpha_s$ 线性无关的充分条件是
$\text{A.}$ $\alpha_1, \alpha_2 \cdots, \alpha_s$ 均不为零向量
$\text{B.}$ $\alpha_1, \alpha_2 \cdots, \alpha_s$ 中任意两个向量的分量不成比例
$\text{C.}$ $\alpha_1, \alpha_2 \cdots, \alpha_s$ 中任意一个向量均不能由其余 $s-1$ 个向量线性表示
$\text{D.}$ $\alpha_1, \alpha_2 \cdots, \alpha_s$ 中有一部分向量线性无关
设 $A$ 为 $n$ 阶可逆矩阵, $A^*$ 是 $A$ 的伴随矩阵,则 $\left|A^*\right|=$
$\text{A.}$ $|A|^{n-1}$
$\text{B.}$ $|A|$
$\text{C.}$ $|A|^n$
$\text{D.}$ $|A|^{-1}$
设 $A, B$ 为两随机事件,且 $B \subset A$ ,则下列式子正确的是
$\text{A.}$ $P(A+B)=P(A)$
$\text{B.}$ $P(A B)=P(A)$
$\text{C.}$ $P(B \mid A)=P(B)$
$\text{D.}$ $P(B-A)=P(B)-P(A)$
已知随机变量 $\boldsymbol{X}$ 服从二项分布,且$E(X)=2.4, \quad D(X)=1.44 $ 则二项分布的参数 $n, p$ 的值为
$\text{A.}$ $n=4, \quad p=0.6$
$\text{B.}$ $n=6, \quad p=0.4$
$\text{C.}$ $n=8, \quad p=0.3$
$\text{D.}$ $n=24, \quad p=0.1$
设随机变量 $\boldsymbol{X}$ 和 $Y$ 相互独立,其概率分布为
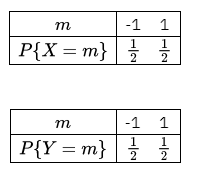
则下列式子正确的是
$\text{A.}$ $X=Y$
$\text{B.}$ $P\{X=Y\}=0$
$\text{C.}$ $P\{X=Y\}=\frac{1}{2}$
$\text{D.}$ $P\{X=Y\}=1$
填空题 (共 6 题 ),请把答案直接填写在答题纸上
极限 $L=\lim _{n \rightarrow \infty}(\sqrt{n+3 \sqrt{n}}-\sqrt{n-\sqrt{n}})=$
设函数 $f(x)$ 有连续的导函数, $f(0)=0$ 且 $f^{\prime}(0)=b$ ,若函数 $F(x)=\left\{\begin{array}{cl}\frac{f(x)+a \sin x}{x}, & x \neq 0 \\ A & x=0\end{array}\right.$ 在 $x=0$ 处连续,则常数 $A=$
曲线 $y=x^2$ 与直线 $y=x+2$ 所围成的平面图形的面积为
若线性方程组 $\left\{\begin{array}{l}x_1+x_2=-a_1 \\ x_2+x_3=a_2 \\ x_3+x_4=-a_3 \\ x_4+x_1=a_4\end{array}\right.$ 有解, 则常数 $a_1, a_2, a_3, a_4$应满足条件
一射手对同一目标独立的进行四次射击,若至少命中一次的概率为 $\frac{80}{81}$ ,则射手的命中率为
已知随机变量 $X \sim N(-3,1), Y \sim N(2,1)$, 且 $X, Y$ 相互独立,设随机变量 $Z=X-2 Y+7$ ,则 $Z \sim$
解答题 (共 19 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
求极限 $I=\lim _{x \rightarrow \infty} \frac{1}{x} \int_0^x\left(1+t^2\right) e^{t^2-x^2} \mathrm{~d} t$.
求不定积分 $\int \frac{x \cos ^4 \frac{x}{2}}{\sin ^3 x} \mathrm{~d} x$.
证明不等式
$$
1+x \ln \left(x+\sqrt{1+x^2}\right) \geq \sqrt{1+x^2}(-\infty < x < +\infty)
$$
求函数 $I(x)=\int_e^x \frac{\ln t}{t^2-2 t+1} \mathrm{~d} t$ 在区间 $\left[e, e^2\right]$ 上的最大值.
设 $x^2+z^2=y \varphi\left(\frac{z}{y}\right)$ ,其中 $\varphi$ 为可微函数,求 $\frac{\partial z}{\partial y}$.
计算 $\iint_D x e^{-y^2} \mathrm{~d} x \mathrm{~d} y$ ,其中 $D$ 是曲线 $y=4 x^2$ 和 $y=9 x^2$ 在第一象限所围成的区域.
求级数 $\sum_{n=1}^{\infty} \frac{(x-3)^n}{n^2}$ 的收敛域.
求微分方程 $y^{\prime}+y \cos x=(\ln x) e^{-\sin x}$ 的通解.
某公司可通过电台和报纸两种方式做销售某种商品广告,根据统计资料,销售收入 $R$ (万元) 与电台广告费用 $x_1$ (万元)及报纸广告费用 $x_2$ (万元)之间的关系有如下经验公式:
$$
R=15+14 x_1+32 x_2-8 x_1 x_2-2 x_1^2-10 x_2^2 \text {. }
$$
(1)在广告费用不限的情况下, 求最优广告策略;
(2)若提供的广告费用为 1.5 万元, 求相应的最优广告策略.
设 $f(x)$ 在闭区间 $[0, c]$ 上连续,其导数 $f^{\prime}(x)$ 在开区间 $(0, c)$ 内存在,且单调减少, $f(0)=0$ ,试应用拉格郎日中值定理证明不等式 $f(a+b) \leq f(a)+f(b)$ ,其中常数 $a, b$ 满足条件 $0 \leq a \leq b \leq a+b \leq c$.
设 $A$ 为 $10 \times 10$ 矩阵 $\left[\begin{array}{ccccc}0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 \\ \cdots & \cdots & \cdots & \cdots & \cdots \\ 0 & 0 & 0 & 0 & 1 \\ 10^{10} & 0 & 0 & 0 & 0\end{array}\right]$ ,计算行列
式 $|A-\lambda E|$ ,其中 $E$ 是 10 阶单位矩阵, $\lambda$ 为常数.
设方阵 $A$ 满足条件 $A^T A=E$ ,其中 $A^T$ 是 $A$ 的转置矩阵, $E$ 为单位阵,试证明所对应的特征值的绝对值等于 1 .
已知线性方程组 $\left\{\begin{array}{l}x_1+x_2+x_3+x_4+x_5=a \\ 3 x_1+2 x_2+x_3+x_4-3 x_5=0 \\ x_2+2 x_3+2 x_4+6 x_5=b \\ 5 x_1+4 x_2+3 x_3+3 x_4-x_5=2\end{array}\right.$
(1) 问 $a, b$ 为何值时,方程组有解?
(2) 方程组有解时,求出方程组的导出组的一个基础解系;
(3) 方程组有解时, 求出方程组的全部解.
已知对于 $n$ 阶方阵 $A$ ,存在自然数 $k$ ,使得 $A^k=0$ 试证明矩阵 $E-A$ 可逆,并写出其逆矩阵的表达式 ( $E$ 为 $n$ 阶单位阵) .
设 $A$ 为 $n$ 阶矩阵, $\lambda_1$ 和 $\lambda_2$ 是 $A$ 的两个不同的特征值, $x_1, x_2$ 是分别属于 $\lambda_1$ 和 $\lambda_2$ 的特征向量,试证明: $x_1+x_2$ 不是 $\boldsymbol{A}$ 的特征向量.
从 $0,1,2, \cdots, 9$ 等十个数字中任意选出三个不同的数字,试求下列事件的概率:
$A_1=$ “三个数字中不含 0 和 5 ”; $A_2=$ “三个数字中含 0 但不含 5 "
一电子仪器由两个部件构成,以 $\boldsymbol{X}$ 和 $\boldsymbol{Y}$ 分别表示两个部件的寿命(单位:千小时),已知 $X$ 和 $Y$ 的联合分布函数为:
$$
F(x, y)=\left\{\begin{array}{cc}
1-e^{-0.5 x}-e^{-0.5 y}+e^{-0.5(x+y)} & x \geq 0, y \geq 0 \\
0 & \text { 其他 }
\end{array} .\right.
$$
(1) 问 $X$ 和 $Y$ 是否独立?
(2) 求两个部件的寿命都超过 100 小时的概率 $\alpha$.
甲乙两人独立地各进行两次射击,假设甲的命中率为 0.2 ,乙的为 0.5 , 以 $X$ 和 $Y$ 分别表示甲和乙的命中次数,试求 $X$ 和 $\boldsymbol{Y}$ 联合概率分布.
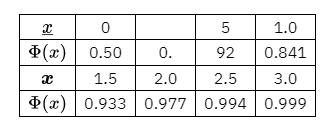
某地抽样调查结果表明,考生的外语成绩(百分制)近似服从正态分布,平均成绩为 72 分, 96 分以上的占考生总数的 $2.3 \%$ ,试求考生的外语成绩在 60 分至 84 分之间的概率.
[附表] (表中 $\Phi(x)$ 是标准正态分布函数)