单选题 (共 10 题 ),每题只有一个选项正确
$-6$ 的相反数是 ( )
$\text{A.}$ $-\frac{1}{6}$
$\text{B.}$ $-6$
$\text{C.}$ $\frac{1}{6}$
$\text{D.}$ $6$
下列说法中, 正确的是 ( )
$\text{A.}$ 调查某班 45 名学生的身高情况宜采用全面调查
$\text{B.}$ “太阳东升西落” 是不可能事件
$\text{C.}$ 为了直观地介绍空气各成分的百分比, 最适合使用的统计图是条形统计图
$\text{D.}$ 任意投掷一枚质地均匀的硬币 26 次, 出现正面朝上的次数一定是 13 次
下列计算正确的是()
$\text{A.}$ $\mathrm{a}^{7} \div \mathrm{a}^{5}=\mathrm{a}^{2}$
$\text{B.}$ $5 a-4 a=1$
$\text{C.}$ $3 a^{2} \cdot 2 a^{3}=6 a^{6}$
$\text{D.}$ $(a-b)^{2}=a^{2}-b^{2}$
在平面直角坐标系中, 点 $(5,1)$ 关于原点对称的点的坐标是 ( )
$\text{A.}$ $(-5,1)$
$\text{B.}$ $(5,-1)$
$\text{C.}$ $(1,5)$
$\text{D.}$ $(-5,-1)$
《义务教育课程标准 (2022 年版)》首次把学生学会炒菜纳入劳动教育课程, 并做出 明确规定. 某班有 7 名学生已经学会炒的菜品的种数依次为: $3,5,4,6,3,3,4$. 则 这组数据的众数和中位数分别是( )
$\text{A.}$ 3,4
$\text{B.}$ 4,3
$\text{C.}$ 3,3
$\text{D.}$ 4,4
为落实 “双减” 政策, 某校利用课后服务开展了主题为 “书香满校园”的读书活动. 现需购买甲, 乙两种读本共 100 本供学生阅读, 其中甲种读本的单价为 10 元/本, 乙 种读本的单价为 8 元/本, 设购买甲种读本 $x$ 本,则购买乙种读本的费用为( )
$\text{A.}$ $8 x$ 元
$\text{B.}$ $10(100-x)$ 元
$\text{C.}$ $8(100-x)$ 元
$\text{D.}$ $(100-8 x)$ 元
如图, $A B / / C D, A E / / C F, \angle B A E=75^{\circ}$, 则 $\angle D C F$ 的度数为 $(\quad)$

$\text{A.}$ $65^{\circ}$
$\text{B.}$ $70^{\circ}$
$\text{C.}$ $75^{\circ}$
$\text{D.}$ $105^{\circ}$
如图, $P A, P B$ 是 $\odot 0$ 的切线, $A 、 B$ 为切点, 若 $\angle A O B=128^{\circ}$, 则 $\angle P$ 的度数为 ( )
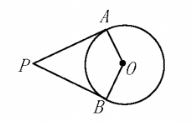
$\text{A.}$ $32^{\circ}$
$\text{B.}$ $52^{\circ}$
$\text{C.}$ $64^{\circ}$
$\text{D.}$ $72^{\circ}$
如图, 在 $\triangle \mathrm{ABC}$ 中, 按以下步骤作图:
(1) 分别以点 $A 、 B$ 为圆心, 大于 $\frac{1}{2} \mathrm{AB}$ 的长为半径画弧, 两弧交于 $P 、 Q$ 两点;
(2)作直线 $P Q$ 交 $A B$ 于点 $D$;
(3) 以点 $D$ 为圆心, $A D$ 长为半径画弧交 $P Q$ 于点 $M$, 连接 $A M 、 B M$.
若 $A B=2 \sqrt{2}$, 则 $A M$ 的长为
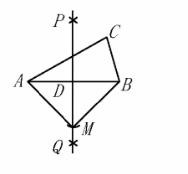
$\text{A.}$ $4$
$\text{B.}$ $2$
$\text{C.}$ $\sqrt{3}$
$\text{D.}$ $\sqrt{2}$
填空题 (共 6 题 ),请把答案直接填写在答题纸上
若式子 $\sqrt{x-19}$ 在实数范围内有意义, 则实数的取值范围是
分式方程 $\frac{2}{x}=\frac{5}{x+3}$ 的解为
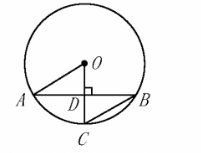
如图, $A 、 B 、 C$ 是 $\odot O$ 上的点, $O C \perp A B$, 垂足为点 $D$, 且 $D$ 为 $O C$ 的中点, 若 $O A=7$, 则 $\mathrm{BC}$ 的长为
关于 $x$ 的一元二次方程 $x^{2}+2 x+\mathrm{t}=0$ 有两个相等的实数根, 则实数 $\mathrm{t}$ 的值为
为了解某校学生对湖南省 “强省会战略”的知晓情况, 从该校全体 1000 名学生中, 随机抽取了 100 名学生进行调查, 结果显示有 95 名学生知晓. 由此, 估计该校全体学 生中知晓湖南省“强省会战略”的学生有 ( ) 名.
当今大数据时代, “二维码” 具有存储量大. 保密性强、追踪性高等特点, 它已被 广泛应用于我们的日常生活中, 尤其在全球 “新冠”疫情防控期间, 区区 “二维码” 已经展现出无穷威力. 看似 “码码相同” , 实则 “码码不同”. 通常, 一个 “二维码” 由 1000 个大大小小的黑白小方格组成, 其中大约 $80 \%$ 的小方格专门用做纠错码和其他 用途的编码, 这相当于 1000 个方格只有 200 个方格作为数据码. 根据相关数学知识, 这 200 个方格可以生成 $2^{200}$ 个不同的数据二维码, 现有四名网友对 $2^{200}$ 的理解如下: YYDS(永远的神): $2^{200}$ 就是 200 个 2 相乘, 它是一个非常非常大的数;
$\operatorname{DDDD}$ (懂的都懂) : $2^{200}$ 等于 $200^{2}$;
JXND(觉醒年代): $2^{200}$ 的个位数字是 6 ;
QGYW (强国有我): 我知道 $2^{10}=1024,10^{3}=1000$, 所以我估计 $2^{200}$ 比 $10^{60}$ 大,
其中对 $2^{200}$ 的理解错误的网友是 ( ) (填写网名字母代号).
解答题 (共 9 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
计算: $|-4|+\left(\frac{1}{3}\right)^{-1}-(\sqrt{2})^{2}+2035^{\circ}$.
解不等式组: $\left\{\begin{array}{l}3 x>-8-x(1) \\ 2(x-1) \leq 62\end{array}\right.$
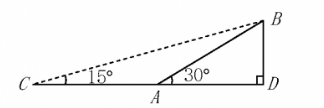
为了进一步改善人居环境, 提高居民生活的幸福指数. 某小区物业公司决定对小区 环境进行优化改造. 如图, $\mathrm{AB}$ 表示该小区一段长为 $20 \mathrm{~m}$ 的斜坡, 坡角 $\angle \mathrm{BAD}=30^{\circ}$, $B D \perp A D$ 于点 $D$. 为方便通行, 在不改变斜坡高度的情况下, 把坡角降为 $15^{\circ}$.
(1) 求该斜坡的高度 BD;
(2) 求斜坡新起点 $\mathrm{C}$ 与原起点 $\mathrm{A}$ 之间的距离. (假设图中 $\mathrm{C}, \mathrm{A}, \mathrm{D}$ 三点共线)
2022 年 3 月 22 日至 28 日是第三十五届 “中国水周”, 在此期间, 某校举行了主 题为 “推进地下水超采综合治理, 复苏河湖生态环境” 的水资源保护知识竞赛. 为了了 解本次知识竞赛成绩的分布情况, 从参赛学生中随机抽取了 150 名学生的初赛成绩进 行统计, 得到如下两幅不完整的统计图表.

(1) 表中 $\mathrm{a}= $ , $b= $ ,$\mathrm{c}= $
(2) 请补全频数分布直方图;
(3) 若某班恰有 3 名女生和 1 名男生的初赛成绩均为 99 分, 从这 4 名学生中随机选取2 名学生参加复赛, 请用列表法或画树状图法求选出的 2 名学生恰好为一名男生、 名女生的概率.
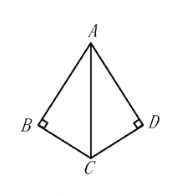
如图, $A C$ 平分 $\angle B A D, C B \perp A B, C D \perp A D$, 垂足分别为 $B, D$.
(1)求证: $\triangle A B C \cong \triangle A D C$;
(2) 若 $\mathrm{AB}=4, \mathrm{CD}=3$, 求四边形 $\mathrm{ABCD}$ 的面积.
22. 电影《刘三姐》中, 有这样一个场景, 罗秀才摇头晃脑地吟唱道: “三百条狗交给 你, 一少三多四下分, 不要双数要单数, 看你怎样分得匀? 该歌词表达的是一道数 学题。其大意是: 把 300 条狗分成 4 群, 每个群里, 狗的数量都是奇数, 其中一个群, 狗的数量少; 另外三个群, 狗的数量多且数量相同。问:应该如何分? 请你根据题意 解答下列问题:
(一)刘三姐的姐妺们以对歌的形式给出答案: “九十九条打猎去, 九十九条看羊来, 九 十九条守门口, 剩下三条给财主.” 请你根据以上信息, 判断以下三种说法是否正确, 在题后相应的括号内, 正确的打 $\checkmark $, 错误的打 $\times $.
(1) 刘三姐的姐妺们给出的答案是正确的, 但不是唯一正确的答案. ( )
(2)刘三姐的姐妺们给出的答案是唯一正确的答案. ( )
(3)该歌词表达的数学题的正确答案有无数多种. ( )
(二)若罗秀才再增加一个条件: “数量多且数量相同的三个群里, 每个群里狗的数量比 数量较少的那个群里狗的数量多 40 条”, 求每个群里狗的数量.
如图, 在 $\square \mathrm{ABCD}$ 中, 对角线 $\mathrm{AC}, \mathrm{BD}$ 相交于点 $0, \mathrm{AB}=\mathrm{AD}$.
(1) 求证: $\mathrm{AC} \perp \mathrm{BD}$;
(2) 若点 $\mathrm{E}, \mathrm{F}$ 分别为 $\mathrm{AD}, \mathrm{A} 0$ 的中点, 连接 $\mathrm{EF}, \mathrm{EF}=\frac{3}{2}, \mathrm{AO}=2$, 求 $\mathrm{BD}$ 的长及四边形 $\mathrm{ABCD}$ 的周长.

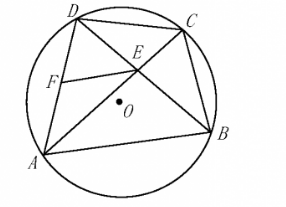
如图, 四边形 $\mathrm{ABCD}$ 内接于 $\odot 0$, 对角线 $\mathrm{AC}, \mathrm{BD}$ 相交于点 $\mathrm{E}$, 点 $\mathrm{F}$ 在边 $\mathrm{AD}$ 上, 连 接 EF.
(1) 求证: $\triangle \mathrm{ABE} \sim \triangle \mathrm{DCE}$;
(2) 当 $\widehat{\mathrm{DC}}=\widehat{\mathrm{CB}}, \angle \mathrm{DFE}=2 \angle \mathrm{CDB}$ 时, 则 $\frac{\mathrm{AE}}{\mathrm{BE}}-\frac{\mathrm{DE}}{\mathrm{CE}}= ; \frac{\mathrm{AF}}{\mathrm{AB}}+\frac{\mathrm{FE}}{\mathrm{AD}}=$; $\frac{1}{\mathrm{AB}}+\frac{1}{\mathrm{AD}}-\frac{1}{\mathrm{AF}}=$ (直接将结果填写在相应的横线上)
(3) (1)记四边形 $\mathrm{ABCD}, \triangle \mathrm{ABE}, \triangle \mathrm{CDE}$ 的面积依次为 $\mathrm{S}, \mathrm{S}_{1}, \mathrm{~S}_{2}$, 若满足 $\sqrt{\mathrm{S}}=\sqrt{\mathrm{S}_{1}}+\sqrt{\mathrm{S}_{2}}$,
试判断 $\triangle A B E, \triangle C D E$ 的形状, 并说明理由.
(2)当 $\widehat{D C}=\widehat{C B}, A B=m, A D=n, C D=p$ 时, 试用含 $m, n, p$ 的式子表示 $A E \cdot C E$.
若关于 $x$ 的函数 $\mathrm{y}$, 当 $\mathrm{t}-\frac{1}{2} \leqslant x \leqslant \mathrm{t}+\frac{1}{2}$ 时, 函数 $\mathrm{y}$ 的最大值为 $\mathrm{M}$, 最小值为 $\mathrm{N}$, 令函数 $\mathrm{h}=\frac{\mathrm{M}-\mathrm{N}}{2}$, 我们不妨把函数 $\mathrm{h}$ 称之为函数 $\mathrm{y}$ 的 “共同体函数”.
(1) (1) 若函数 $\mathrm{y}=4044 x$, 当 $\mathrm{t}=1$ 时, 求函数 $\mathrm{y}$ 的 “共同体函数” $\mathrm{h}$ 的值;
(2)若函数 $\mathrm{y}=\mathrm{k} x+\mathrm{b}(\mathrm{k} \neq 0, \mathrm{k} , \mathrm{~b}$ 为常数),求函数 $\mathrm{y}$ 的 “共同体函数” $\mathrm{h}$ 的解析式;
(2) 若函数 $\mathrm{y}=\frac{2}{x}(x \geqslant 1)$, 求函数 $\mathrm{y}$ 的 “共同体函数” $\mathrm{h}$ 的最大值;
(3) 若函数 $\mathrm{y}=-x^{2}+4 x+\mathrm{k}$ ,是否存在实数 $\mathrm{k}$, 使得函数 $\mathrm{y}$ 的最大值等于函数 $\mathrm{y}$ 的 “共同 体函数” $\mathrm{h}$ 的最小值, 若存在, 求出 $\mathrm{k}$ 的值; 若不存在, 请说明理由.