单选题 （共 8 题 ），每题只有一个选项正确
命题 “ $\forall x>0, x \geqslant 1$ ” 的否定是
$\text{A.}$ $\forall x>0, \quad x < 1 $
$\text{B.}$ $\exists x>0, x < 1$
$\text{C.}$ $\exists x \leqslant 0, \quad x < 1$
$\text{D.}$ $\exists x \leqslant 0, \quad x \geqslant 1$
小明有 50 元钱去买水果, 他发现如果买 $1 \mathrm{~kg}$ 阳光玫瑰和 $750 \mathrm{~g}$ 涌泉蜜桔则钱不够, 若买 $1.2 \mathrm{~kg}$ 阳光玫瑰和 $400 \mathrm{~g}$ 涌泉蜜桔则钱有余, 设 $800 \mathrm{~g}$ 阳光玫瑰与 $1.4 \mathrm{~kg}$ 涌泉蜜桔的价格分别为 $a, b$ (单位:元), 则
$\text{A.}$ $a < b$
$\text{B.}$ $a>b$
$\text{C.}$ $a=b$
$\text{D.}$ $a, b$ 大小无法比较
下列方程中不能用二分法求近似解的为
$\text{A.}$ $\ln x+x=0$
$\text{B.}$ $\mathrm{e}^x-3 x=0$
$\text{C.}$ $x^3-3 x+1=0$
$\text{D.}$ $4 x^2-4 \sqrt{5} x+5=0$
函数 $f(x)=\log _2(2 x) \cdot \log _2(4 x)$ 的值域为
$\text{A.}$ $\mathbf{R}$
$\text{B.}$ $\left[-\frac{1}{24},+\infty\right)$
$\text{C.}$ $\left[-\frac{1}{4},+\infty\right)$
$\text{D.}$ $\left[-\frac{3}{2},+\infty\right)$
函数 $f(x)=2^x+3^{-x}$ 的图象可能为
$\text{A.}$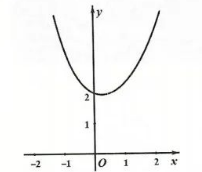 
$\text{B.}$ 
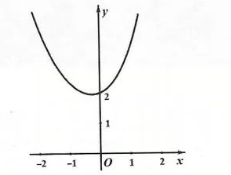$\text{C.}$ 
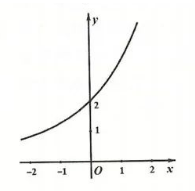$\text{D.}$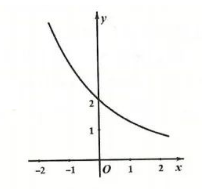 
已知集合 $A=(a, b)$, 集合 $B=(c, d)$, 则 “ $a < d$ 且 $b>c$ ”是“ $A \cap B \neq \varnothing$ ”成立的
$\text{A.}$ 充分不必要条件
$\text{B.}$ 必要不充分条件
$\text{C.}$ 充要条件
$\text{D.}$ 既不充分又不必要条件
已知 $a>b>0$ 且 $a^2-b^2=4$, 则 $a^2-a b+b^2$ 的最小值为
$\text{A.}$ $2 \sqrt{2}$
$\text{B.}$ $2 \sqrt{3}$
$\text{C.}$ 4
$\text{D.}$ $2 \sqrt{5}$
已知 $f(x)=\left\{\begin{array}{cc}\left|4-x^2\right|, & x \leqslant 0, \\ \frac{1}{x}, & x>0\end{array}\right.$, 若 $x_1 < x_2 < x_3$ 满足 $f\left(x_1\right)=f\left(x_2\right)=f\left(x_3\right)$, 则 $\frac{x_1 x_2}{x_3}$ 的取值范围为
$\text{A.}$ $(0,2 \sqrt{3}]$
$\text{B.}$ $(0, \sqrt{15}]$
$\text{C.}$ $(0,8]$
$\text{D.}$ $(0,64]$
多选题 （共 4 题 ），每题有多个选项正确
已知集合 $A=\{1,2,3\}, B=\{a+b \mid a, b \in A\}$, 则
$\text{A.}$ 集合 $A$ 有 8 个子集
$\text{B.}$ 集合 $B$ 中有 6 个元素
$\text{C.}$ $A \cup B=\{1,2,3,4,5,6\}$
$\text{D.}$ $A \subseteq B$
一元二次不等式 $a x^2+b x+c>0$ 的解集为 $(-2,1)$, 则
$\text{A.}$ $a < 0$
$\text{B.}$ $c < 0$
$\text{C.}$ $a+b+c=0$
$\text{D.}$ $a-b+2 c>0$
已知 $x=\log _a b, y=a^b, z=b^a$, 则下列不等式可能成立的为
$\text{A.}$ $y>z>x>1$
$\text{B.}$ $z>y>x>1$
$\text{C.}$ $y < z < x < 1$
$\text{D.}$ $z < y < x < 1$
已知定义在 $\mathbf{R}$ 上的函数 $f(x)$ 的图象为一条连续不断的曲线, 且关于点 $(a, b)$ 与 $(b, a)$ 对称 $(a \neq b)$, 则
$\text{A.}$ 存在非零实数 $T$ 使 $f(x+T)=f(x)$
$\text{B.}$ 函数 $y=f(x)$ 必有零点
$\text{C.}$ 存在实数 $t$ 使 $f(t)=t$
$\text{D.}$ 存在实数 $t$ 使 $f(t)=-t$
填空题 （共 4 题 ），请把答案直接填写在答题纸上
已知幂函数 $f(x)=\left(2 m^2+m\right) x^{m-1}$ 是偶函数, 则 $m=$
计算: $3^{\log _3 2}+\log _4 3 \cdot \log _3 8=$
已知定义在 $\mathbf{R}$ 上的函数 $f(x)$ 满足 $f(x)+x f(-x)=x^2+x$,则函数 $f(x)$ 的解析式 $f(x)=$
已知实数 $a, b$ 满足 $2^{a-2}+a=\frac{1}{2}, \frac{1}{2} b^2+\log _2 b=-\frac{3}{4}$, 则 $\frac{2^a}{b^2}=$
解答题 （共 6 题 ），解答过程应写出必要的文字说明、证明过程或演算步骤
已知集合 $A=\{x|| 2 x+1| < | x-4 \mid\}, B=\left\{x \mid \frac{1}{x+a} < 1\right\}$.
(I) 求集合 $A$;
(II) 若 $A \subseteq B$, 求实数 $a$ 的取值范围.
已知 $x_1, x_2$ 是方程 $x^2-b x+c=0$ 的实数解.
(I) 若 $c>-2, x_1=1$, 求 $b+\frac{9}{c+2}$ 的最小值;
(II) 若 $1 \leqslant x_1 \leqslant 2 \leqslant x_2 \leqslant 3$, 求 $\frac{b}{c}$ 的取值范围.
已知函数 $f(x)=\log _{\frac{1}{2}} \frac{1}{2^x+1}+k x$ 为偶函数.
(I) 求实数 $k$ 的值;
(II) 求不等式 $f\left(\log _2 x\right)>f(2)$ 的解集.
通货膨胀率被定义为物价总水平的增长率. 已知某件商品 2015 年 10 月的定价为 21.5 , 而该商品 2023 年 10 月的定价为 22.8 . 该商品的增长率恰与某地区的物价总水平的增长率一致.
(I) 求该地区 2015 年至 2023 年的年平均通货膨胀率;
（II）资金的增长率被称为名义利率, 以欧文 - 费雪(Irving Fisher)（20世纪一位伟大的货币经济学家) 命名的费雪方程式给出了关于实际利率的定义, 费雪方程式表明名义利率等于实际利率加上通货膨胀率. 已知某银行三年期定期存款的利率如下图所示 (银行定期年利率为单利, 三年存款的利息 $=$ 本金*年利率 $* 3$ ).
(i) 求该存款 2020 年至 2023 年的实际年平均利率（精确到 $1 \%$ );
(ii) 若在 2015 年至 2023 年间该存款以同样的年利率 (3.8500\%, 单利) 存五年定期, 则其实际年平均利率与三年定期相比是大还是小? (只写出结论, 不要求证明)
参考数据: $\lg 22.8 \approx 1.3579, \lg 21.5 \approx 1.3324, \lg 1.0385 \approx 0.0164, \lg 1.1155 \approx 0.0475$,
$$
10^{0.00283} \approx 1.0065,10^{0.0031875} \approx 1.0074,10^{0.011875} \approx 1.0277, \quad 10^{0.01583} \approx 1.0371
$$
已知函数 $f(x)=x|x-a|(0 < a < 7)$.
(I) 求函数 $f(x)$ 的单调递减区间;
(II) 若 $\exists b \in \mathbf{R}$, 使不等式 $-x+b \leqslant f(x) \leqslant k x+b$ 对 $\forall x \in[1,7]$ 恒成立, 求 $k$ 的最小值 $g(a)$ 及 $g(a)$的最小值.
定义 1 : 通常我们把一个以集合作为元素的集合称为族(collection).
定义 2: 集合 $X$ 上的一个拓扑(topology)乃是 $X$ 的子集为元素的一个族 $\Gamma$, 它满足以下条件: (1) $\varnothing$ 和 $X$ 在 $\Gamma$ 中; (2) $\Gamma$ 的任意子集的元素的并在 $\Gamma$ 中; (3) $\Gamma$ 的任意有限子集的元素的交在 $\Gamma$ 中.
(I) 族 $P=\{\varnothing, X\}$, 族 $Q=\{x \mid x \subseteq X\}$, 判断族 $P$ 与族 $Q$ 是否为集合 $X$ 的拓扑;
(II) 设有限集 $X$ 为全集.
(i) 证明: $\complement_X\left(A_1 \cap A_2 \cap \cdots \cap A_n\right)=\left(\complement_X A_1\right) \cup\left(\complement_X A_2\right) \cup \cdots \cup\left(\complement_X A_n\right)\left(n \in \mathbf{N}^*\right)$;
(ii) 族 $\Gamma$ 为集合 $X$ 上的一个拓扑, 证明: 由族 $\Gamma$ 所有元素的补集构成的族 $\Gamma_f$ 为集合 $X$ 上的一个拓扑.