单选题 (共 8 题 ),每题只有一个选项正确
如图, 在平行六面体 (底面为平行四边形的四棱柱) $A B C D-A_1 B_1 C_1 D_1$ 中, $E$ 为 $B C$ 延长线上一点, $\overrightarrow{B C}=2 \overrightarrow{C E}$, 则 $\overrightarrow{D_1 E}$ 为
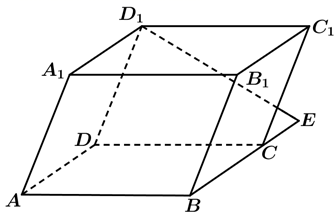
$\text{A.}$ $\overrightarrow{A B}+\overrightarrow{A D}+\overrightarrow{A A_1}$
$\text{B.}$ $\overrightarrow{A B}+\frac{1}{2} \overrightarrow{A D}-\overrightarrow{A A_1}$
$\text{C.}$ $\overrightarrow{A B}+\overrightarrow{A D}+\overrightarrow{A A_1}$
$\text{D.}$ $\overrightarrow{A B}+\frac{1}{3} \overrightarrow{A D}-\overrightarrow{A A_1}$
已知等比数列 $\left\{a_n\right\}$ 中, $a_3+a_5+\cdots+a_{2 k+1}=84, a_2+a_4+\cdots+a_{2 k}=42, k \in \mathbf{N}_{+}$, 则公比 $q=$
$\text{A.}$ 5
$\text{B.}$ 4
$\text{C.}$ 3
$\text{D.}$ 2
在二面角的棱上有两个点 $A 、 B$, 线段 $A C 、 B D$ 分别在这个二面角的两个面内, 并且都垂直于棱 $A B$, 若 $A B=1$, $A C=2, B D=3, C D=2 \sqrt{2}$, 则这个二面角的大小为
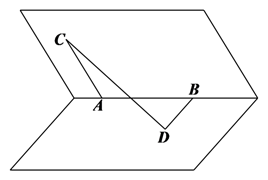
$\text{A.}$ $30^{\circ}$
$\text{B.}$ $45^{\circ}$
$\text{C.}$ $60^{\circ}$
$\text{D.}$ $90^{\circ}$
已知等差数列 $\left\{a_n\right\}$ 的前 $n$ 项和为 $S_n$, 若 $S_2=5, S_5=2$, 则 $S_7=$
$\text{A.}$ -5
$\text{B.}$ -6-
$\text{C.}$ -7
$\text{D.}$ -8
已知直线 $l_1$ 的方程为: $x+a y-2=0$, 直线 $l_2$ 的方程为: $2 x-y+1=0$, 若 $l_1 \perp l_2$, 则直线 $l_1$ 与 $l_2$ 的交 点坐标为
$\text{A.}$ $\left(-\frac{4}{3},-\frac{5}{3}\right)$
$\text{B.}$ $(0,1)$
$\text{C.}$ $(2,5)$
$\text{D.}$ $\left(\frac{3}{4}, \frac{5}{2}\right)$
已知抛物线 $C: y^2=2 p x(p>0)$ 的焦点为 $F$, 抛物线 $C$ 上的两点 $P, Q$ 均在第一象限, 且 $|P Q|=2,|P F|=3$, $|Q F|=4$, 则直线 $P Q$ 的斜率为
$\text{A.}$ 1
$\text{B.}$ $\sqrt{2}$
$\text{C.}$ $\sqrt{3}$
$\text{D.}$ $\sqrt{5}$
已知从点 $A(6,1)$ 射出的光线经直线 $x+y+1=0$ 上的点 $M$ 反射后经过点 $B(3,2)$, 则 $|A M|+|B M|=$
$\text{A.}$ $\sqrt{10}$
$\text{B.}$ $\sqrt{106}$
$\text{C.}$ $\sqrt{105}$
$\text{D.}$ $3 \sqrt{10}$
已知双曲线 $C: \frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0, b>0)$ 的左、右焦点分别为 $F_1, F_2, O$ 为坐标原点, $P$ 为双曲线在第一象限 上的点, 直线 $P O 、 P F_2$ 分别交双曲线 $C$ 的左、右支于 $M, N$, 若 $\left|P F_1\right|=3\left|P F_2\right|$, 且 $\angle M F_2 N=120^{\circ}$, 则双曲 线的离心率为
$\text{A.}$ $\frac{\sqrt{5}}{2}$
$\text{B.}$ $\frac{\sqrt{13}}{2}$
$\text{C.}$ 3
$\text{D.}$ 2
多选题 (共 4 题 ),每题有多个选项正确
关于方程 $\frac{x^2}{m-3}+\frac{y^2}{11-m}=1(m \neq 3$ 且 $m \neq 11)$ 所对应的图形, 下列说法正确的是
$\text{A.}$ 若方程表示一个圆, 则 $m=7$
$\text{B.}$ 无论 $m$ 为何值时, 该方程只可能表示一个圆或一个椭圆
$\text{C.}$ 当 $3 < m < 7$ 时, 方程表示一个焦点在 $x$ 轴上的椭圆
$\text{D.}$ 当 $3 < m < 7$ 时, 方程表示一个焦点在 $y$ 轴上的椭圆
等差数列 $\left\{a_n\right\}$ 中, 已知 $S_6>S_7, S_7 < S_8$, 则正确的结论是
$\text{A.}$ $a_1 < 0$
$\text{B.}$ $d < 0$
$\text{C.}$ $S_7$ 是 $S_n$ 中最小值
$\text{D.}$ $S_9>S_6$
下列结论错误的是
$\text{A.}$ 直线 $(3+m) x+4 y-3+3 m=0(m \in R)$ 恒过定点 $(-3,-3)$
$\text{B.}$ 直线 $\sqrt{3} x+y+1=0$ 的倾斜角为 $150^{\circ}$
$\text{C.}$ 圆 $x^2+y^2=4$ 上有且仅有 3 个点到直线 $l: x-y+\sqrt{2}=0$ 的距离都等于 1
$\text{D.}$ 与圆 $(x-2)^2+y^2=2$ 相切, 且在 $x$ 轴、 $y$ 轴上的截距相等的直线有两条
已知抛物线 $C: x^2=2 p y$ 的焦点坐标为 $F$, 过点 $F$ 的直线与抛物线相交于 $A, B$ 两点, 点 $\left(\sqrt{2}, \frac{1}{2}\right)$ 在抛物线 上. 则
$\text{A.}$ $p=1$
$\text{B.}$ 当 $A B \perp y$ 轴时, $|A B|=4$
$\text{C.}$ $\frac{1}{|A F|}+\frac{1}{|B F|}$ 为定值 1
$\text{D.}$ 若 $\overrightarrow{A F}=2 \overrightarrow{F B}$, 则直线 $A B$ 的斜率为 $\pm \frac{\sqrt{2}}{4}$
填空题 (共 4 题 ),请把答案直接填写在答题纸上
已知双曲线 $\frac{x^2}{4}-\frac{y^2}{5}=1$ 和圆 $x^2+y^2-8 x+15=0$, 则圆心 $C$ 到双曲线渐近线的距离为
在数列 $\left\{a_n\right\}$ 中, 若 $a_1=2, a_{n+1}=1-\frac{1}{a_n}$, 则 $a_{2020}=$
圆 $C_1: x^2+y^2=9$ 与圆 $C_2: x^2+y^2+x+2 y-4=0$ 的公共弦长为
已知抛物线 $C: y^2=2 p x(p>0)$ 的焦点为 $F$, 准线 $l: x=-1$, 点 $M$ 在抛物线 $C$ 上, 点 $M$ 在直线 $l: x=-1$ 上的射影为 $A$, 且直线 $A F$ 的斜率为 $-\sqrt{3}$, 则 $\triangle M A F$ 的面积为
解答题 (共 6 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
记 $S_n$ 是等差数列 $\left\{a_n\right\}$ 的前 $n$ 项和, 若 $S_5=-35, S_7=-21$.
(1) 求 $\left\{a_n\right\}$ 的通项公式, 并求 $S_n$ 的最小值;
(2) 设 $b_n=\left|a_n\right|$, 求数列 $\left\{b_n\right\}$ 的前 $n$ 项和 $T_n$.
在如图所示的几何体中, 四边形 $A B C D$ 为矩形, 平面 $A B E F \perp$ 平面 $A B C D, E F / / A B, \angle B A F=90^{\circ},|A D|=$ $4,|A B|=|A F|=2|E F|=2$, 点 $P$ 在线段 $D F$ 上.
(1) 若 $P$ 是 $D F$ 的中点, 求异面直线 $B E$ 与 $C P$ 所成角的余弦值;
(2) 是否存在点 $P$, 使得平面 $A D F$ 与平面 $A P C$ 的夹角的余弦值为 $\frac{\sqrt{6}}{3}$ ? 若存在, 求 $P F$ 的长度; 若不存在, 请说明理由.

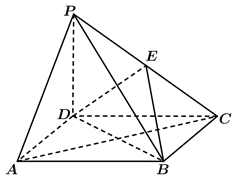
如图, 在四棱雉 $P-A B C D$ 中, 底面 $A B C D$ 是正方形, 侧棱 $P D \perp$ 底面 $A B C D, P D=D C, E$ 是 $P C$ 的中点.
(1) 求 $P B$ 与平面 $B D E$ 所成角的正弦值;
(2) 求点 $A$ 到平面 $B D E$ 的距离.
已知双曲线 $\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a, b>0)$ 的渐近线方程为 $y= \pm \frac{\sqrt{3}}{3}$, 左焦点为 $F(-2,0)$.
(1) 求双曲线 $C$ 的标准方程;
(2) 过点 $Q(2,0)$ 作直线 $l$ 与双曲线 $C$ 右支交于 $A, B$ 两点, 若 $\overrightarrow{A Q}=2 \overrightarrow{Q B}$, 求直线 $l$ 的方程.
已知圆 $C$ 经过点 $A(-1,0)$ 和 $B(5,0)$, 且圆心在直线 $x+2 y-2=0$ 上.
(1) 求圆 $C$ 的标准方程;
(2) 直线 $l$ 过点 $D(-1,1)$, 且与圆 $C$ 相切, 求直线 $l$ 的方程;
(3) 设直线 $l^{\prime}: x+\sqrt{3} y-1=0$ 与圆 $C$ 相交于 $M, N$ 两点, 点 $P$ 为圆 $C$ 上的一动点, 求 $\triangle P M N$ 的面积 $S$ 的最大值.
已知抛物线 $C: y^2=2 p x(p>0)$ 的焦点为 $F$, 点 $M\left(x_0, 4\right)$ 在 $C$ 上, 且 $|M F|=\frac{5 p}{2}$.
(1) 求点 $M$ 的坐标及 $C$ 的方程;
(2) 设动直线 $l$ 与 $C$ 相交于 $A, B$ 两点, 且直线 $M A$ 与 $M B$ 的斜率互为倒数, 试问直线 $l$ 是否恒过定点? 若过, 求 出该点坐标; 若不过, 请说明理由.