单选题 (共 7 题 ),每题只有一个选项正确
负数的概念最早出现在 《九章算术》中,把向东走 $2 \mathrm{~km}$ 记作“- $2 \mathrm{~km}$ ”,向西走 $1 \mathrm{~km}$ 应记作
$\text{A.}$ $-2 \mathrm{~km}$
$\text{B.}$ $-1 \mathrm{~km}$
$\text{C.}$ $1 \mathrm{~km}$
$\text{D.}$ $+2 \mathrm{~km}$
“冰丝带"屋顶上的光伏电站,可输出约 44.8 万度/年的清洁电力. 用科学记数法表示为
$\text{A.}$ $0.448 \times 10^6$ 度
$\text{B.}$ $4.48 \times 10^6$ 度
$\text{C.}$ $44.8 \times 10^4$ 度
$\text{D.}$ $4.48 \times 10^5$ 度
下列运算正确是
$\text{A.}$ $7 a+a=7 a^2$
$\text{B.}$ $5 y^2-2 y^2=3$
$\text{C.}$ $3 a b+2 a b=5 a b$
$\text{D.}$ $m^2 n-2 m n^2=-m n^2$
如图, $A B / / C D , \angle A C B=90^{\circ}$ ,则图中与 $\angle 1$ 互余的角有

$\text{A.}$ 1 个
$\text{B.}$ 2 个
$\text{C.}$ 3 个
$\text{D.}$ 4 个
正比例函数 $y=k x$ 的图象经过点 $(1,3) ,(a, b)(b \neq 0)$ ,则 $\frac{a}{b}$ 的值为
$\text{A.}$ 3
$\text{B.}$ $\frac{1}{3}$
$\text{C.}$ -3
$\text{D.}$ $-\frac{1}{3}$
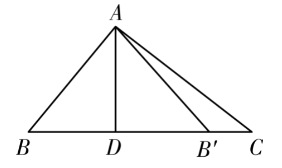
如图,在Rt $\triangle A B C$ 中, $\angle B A C=90^{\circ} , \angle B=50^{\circ} , A D \perp B C$ ,垂足为 $D , \triangle A D B$ 与 $\triangle A D B^{\prime}$ 关于直线 $A D$ 对称,点 $B$ 的对称点是点 $B^{\prime}$ ,则 $\angle C A B^{\prime}$ 的度数为
$\text{A.}$ $10^{\circ}$
$\text{B.}$ $20^{\circ}$
$\text{C.}$ $30^{\circ}$
$\text{D.}$ $40^{\circ}$
二次函数 $y=a x^2-4 a x+c(a>0)$ 的图象过 $A\left(-2, y_1\right) , B\left(0, y_2\right) , C\left(3, y_3\right) , D\left(5, y_4\right)$ 四个点,下列说 法一定正确的是
$\text{A.}$ 若 $y_1 y_2>0$ ,则 $y_3 y_4>0$
$\text{B.}$ 若 $y_1 y_4>0$ ,则 $y_2 y_3>0$
$\text{C.}$ 若 $y_2 y_4 < 0$ ,则 $y_1 y_3 < 0$
$\text{D.}$ 若 $y_3 y_4 < 0$ ,则 $y_1 y_2 < 0$
填空题 (共 5 题 ),请把答案直接填写在答题纸上
实数 $a , b$ 在数轴上对应点的位置如图所示,则 $-a$ $b($ 填$ >, =, < $)
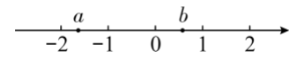
正六边形的一个内角是正 $n$ 边形一个外角的 5 倍,则 $n$ 等于
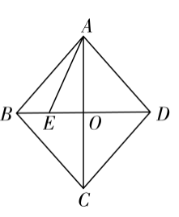
如图,在菱形 $A B C D$ 中,对角线 $A C 、 B D$ 相交于点 $O$ ,点 $E$ 在线段 $B O$ 上,连接 $A E$ ,若 $C D=3 B E$ , $\angle D A E=\angle D E A , E O=1$ ,则线段 $A E$ 的长为
已知反比例函数 $y=\frac{k}{x}(x>0)$ 与 $y=x-1$ 的图象交于点 $P(a, b)$ ,且 $\frac{1}{a}-\frac{1}{b}=-\frac{1}{4}$ ,则 $k$ 的值 是
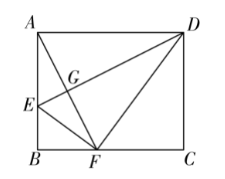
如图,在矩形 $A B C D$ 中, $E$ 为边 $A B$ 上一点,将 $\triangle A D E$ 沿 $D E$ 折叠,使点 $A$ 的对应点 $F$ 恰好落在边 $B C$ 上,连接 $A F$ 交 $D E$ 于点 $G$. 若 $B F \cdot A D=12$ ,则 $A F$ 的长度为
解答题 (共 12 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
计算: $2 \div\left(-\frac{1}{4}\right)-|-\sqrt{18}|+\left(\frac{1}{5}\right)^{-1}$.
解答下列各题.
(1)先化简,再求值: $\left(\frac{x}{x-1}-1\right) \div \frac{x^2-1}{x^2-2 x+1}$ ,其中 $x=\sqrt{5}-1$.
(2)解不等式组: $\left\{\begin{array}{l}3 x-5 \leqslant x+1 \\ 2(2 x-1)>3 x-4\end{array}\right.$ ,并把它的解集在数轴上表示出来.
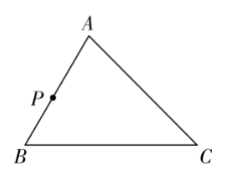
如图,已知 $\triangle A B C , P$ 为边 $A B$ 上一点,请用尺规作图的方法在边 $A C$ 上求作一点 $E$ ,使 $A E+E P=A C$. (保留作图痕迹,不写作法)
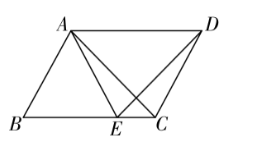
如图,在平行四边形 $A B C D$ 中, $E$ 是 $B C$ 边上一点,连接 $A B 、 A C 、 E D ,$ 若 $A E=A B$ ,求证:
$$
A C=D E
$$
如图,在边长为 1 个单位长度的小正方形组成的网格中,给出了以格点 (网格线的交点) 为端点的线段 $A B$ ,将线段 $A B$ 绕点 $B$ 顺时针旋转 $90^{\circ}$ 得到线段 $A^{\prime} B$.
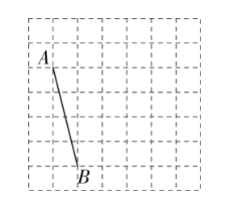
(1)请画出线段 $A^{\prime} B$.
(2)点 $A 、 A^{\prime}$ 之间的距离是?
一张圆桌旁设有 4 个座位,丙先坐在了如图所示的座位上,甲、乙 2 人等可能地坐到(1)、(2)、(3)中的 2 个 座位上.

(1) 甲坐在(1)号座位的概率是
(2)用画树状图或列表的方法,求甲与乙相邻而坐的概率.
一架无人机沿水平直线飞行进行测绘工作,在点 $P$ 处测得正前方水平地面上某建筑物 $A B$ 的顶端 $A$ 的的 俯角为 $30^{\circ}$. 面向 $A B$ 方向继续飞行 5 米,测得该建筑物底端 $B$ 的俯角为 $45^{\circ}$. 已知建筑物 $A B$ 的高为 3 米, 求无人机飞行的高度. (结果精确到 1 米,参考数据: $\sqrt{2} \approx 1.41 , \sqrt{3} \approx 1.73$ )
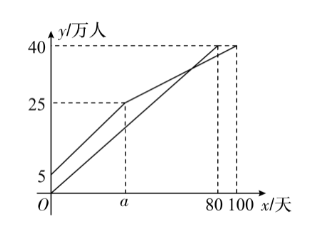
甲乙两地分别对本地各 40 万人接种某种疫苗,甲地在前期完成 5 万人接种后,甲、乙两地同时以相同速 度接种,甲地经过 $a$ 天后接种人数达到 25 万,由于情况变化,接种速度放缓,结果 100 天完成接种任 务,乙地 80 天完成接种任务,在某段时间内,甲、乙两地接种人数 $y$ (万人) 与各自接种时间 $x$ (天) 之间的关系如图所示.
某水果公司以 10 元 $/ \mathrm{kg}$ 的成本价新进 2000 箱荔枝,每箱质量 $5 \mathrm{~kg}$ ,在出售荔枝前,需要去掉损坏的荔枝, 现随机抽取 20 箱,去掉损坏荔枝后称得每箱的质量 (单位: $\mathrm{kg}$ ) 如下:
$\begin{array}{llllllllll}4.7 & 4.8 & 4.6 & 4.5 & 4.8 & 4.9 & 4.8 & 4.7 & 4.8 & 4.7\end{array}$
$\begin{array}{llllllllll}4.8 & 4.9 & 4.7 & 4.8 & 4.5 & 4.7 & 4.7 & 4.9 & 4.7 & 5.0\end{array}$

(1) 直接写出上述表格中 $a , b , c$ 的值.
(2)平均数、众数、中位数都能反映这组数据的集中趋势,请根据以上样本数据分析的结果,任意选 择其中一个统计量,估算这 2000 箱荔枝共损坏了多少千克?
(3 )根据(2)中的结果,求该公司销售这批荔枝每干克定为多少元才不亏本? (结果保留一位小 数)
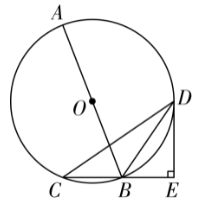
如图, $A B$ 为 $\odot O$ 的直径, $B D , C D$ 是 $\odot O$ 的弦, $\odot O$ 的切线 $D E$ 与 $C B$ 的延长线交于点 $E$ ,且 $D E \perp C E$.
(1) 求证: $\angle C=\angle B D E$.
(2) 若 $C D=3 \sqrt{13} , D E=6$ ,求 $\odot O$ 的直径.
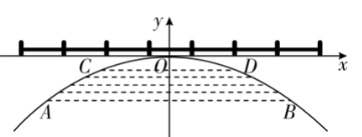
如图,有一座抛物线型拱桥,在正常水位时水面宽 $A B=20 \mathrm{~m}$ ,当水位上升 $3 \mathrm{~m}$ 时,水面宽 $C D=10 \mathrm{~m}$
(1)按如图所示的直角坐标系,求此抛物线的函数表达式.
( 2 )有一条船以 $5 \mathrm{~km} / \mathrm{h}$ 的速度向此桥径直驶来,当船距离此桥 $35 \mathrm{~km}$ ,桥下水位正好在 $A B$ 处,之后 水位每小时上涨 $0.25 \mathrm{~m}$ ,当水位达到 $C D$ 处时,将禁止船只通行. 如果该船的速度不变继续向此 桥行驶 $35 \mathrm{~km}$ 时,水面宽是多少? 它能否安全通过此㮇夰?
解答下列各题.
(1) 问题探究:
如图 1,已知,在四边形 $A B C D$ 中, $A B=B C , A D=D C$ ,则对角线 $A C 、 B D$ 的位置关系 是

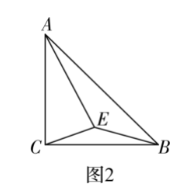
(2) 如图2,已知,在 $\triangle A B C$ 中, $A C=B C , \angle A C B=90^{\circ} . \triangle A B C$ 内一动点 $E$ 到 $A 、 B 、 C$ 三点的 距离之和的最小值为 2 ,求 $A C$ 的长.
(3) 问题解决:
如图3,在平面直角坐标系 $x O y$ 中, $\triangle A B C$ 三个顶点的坐标分别为 $A(-6,0) , B(6,0)$ , $C(0,4 \sqrt{3})$ ,延长 $A C$ 至点 $D$ ,使 $C D=\frac{1}{2} A C$ ,过点 $D$ 作 $D E \perp y$ 轴于点 $E$. 设 $G$ 为 $y$ 轴上一点, 点 $P$ 从点 $E$ 出发,先沿 $y$ 轴到达 $G$ 点,再沿 $G A$ 到达 $A$ 点. 若点 $P$ 在直线 $G A$ 上运动速度为定值 $v$ , 在 $y$ 轴上运动速度为 $2 v$ ,试确定点 $G$ 的位置,使 $P$ 点按照上述要求到达 $A$ 点所用的时间最短,并求 此时点 $G$ 的坐标.
