解答下列各题.
(1) 问题探究:
如图 1,已知,在四边形 $A B C D$ 中, $A B=B C , A D=D C$ ,则对角线 $A C 、 B D$ 的位置关系 是

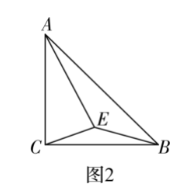
(2) 如图2,已知,在 $\triangle A B C$ 中, $A C=B C , \angle A C B=90^{\circ} . \triangle A B C$ 内一动点 $E$ 到 $A 、 B 、 C$ 三点的 距离之和的最小值为 2 ,求 $A C$ 的长.
(3) 问题解决:
如图3,在平面直角坐标系 $x O y$ 中, $\triangle A B C$ 三个顶点的坐标分别为 $A(-6,0) , B(6,0)$ , $C(0,4 \sqrt{3})$ ,延长 $A C$ 至点 $D$ ,使 $C D=\frac{1}{2} A C$ ,过点 $D$ 作 $D E \perp y$ 轴于点 $E$. 设 $G$ 为 $y$ 轴上一点, 点 $P$ 从点 $E$ 出发,先沿 $y$ 轴到达 $G$ 点,再沿 $G A$ 到达 $A$ 点. 若点 $P$ 在直线 $G A$ 上运动速度为定值 $v$ , 在 $y$ 轴上运动速度为 $2 v$ ,试确定点 $G$ 的位置,使 $P$ 点按照上述要求到达 $A$ 点所用的时间最短,并求 此时点 $G$ 的坐标.

(1) 问题探究:
如图 1,已知,在四边形 $A B C D$ 中, $A B=B C , A D=D C$ ,则对角线 $A C 、 B D$ 的位置关系 是

(2) 如图2,已知,在 $\triangle A B C$ 中, $A C=B C , \angle A C B=90^{\circ} . \triangle A B C$ 内一动点 $E$ 到 $A 、 B 、 C$ 三点的 距离之和的最小值为 2 ,求 $A C$ 的长.

(3) 问题解决:
如图3,在平面直角坐标系 $x O y$ 中, $\triangle A B C$ 三个顶点的坐标分别为 $A(-6,0) , B(6,0)$ , $C(0,4 \sqrt{3})$ ,延长 $A C$ 至点 $D$ ,使 $C D=\frac{1}{2} A C$ ,过点 $D$ 作 $D E \perp y$ 轴于点 $E$. 设 $G$ 为 $y$ 轴上一点, 点 $P$ 从点 $E$ 出发,先沿 $y$ 轴到达 $G$ 点,再沿 $G A$ 到达 $A$ 点. 若点 $P$ 在直线 $G A$ 上运动速度为定值 $v$ , 在 $y$ 轴上运动速度为 $2 v$ ,试确定点 $G$ 的位置,使 $P$ 点按照上述要求到达 $A$ 点所用的时间最短,并求 此时点 $G$ 的坐标.
